O. Schreier - Introduction to Modern Algebra and Matrix Theory

Second Edition

O. SCHREIER
E. SPERNER

Translated by
M ARTIN D AVIS
AND
M ELVIN H AUSNER

DOVER PUBLICATIONS, INC.
Mineola, New York

Bibliographical Note

This Dover edition, first published in 2011, is an unabridged republication of the work originally published in 1959 by Chelsea Publishing Company, New York.

Library of Congress Cataloging-in-Publication Data

Schreier, O. (Otto), 19011929.

[Einfhrung in die analytische Geometeie und Algebra. English]

Introduction to modern algebra and matrix / O. Schreier and E. Sperner. Dover ed.

p. cm.

Originally published: 2nd ed. New York : Chelsea Pub., 1959.

Summary: This unique text provides students with a basic course in both calculus and analytic geometry. It promotes an intuitive approach to calculus and emphasizes algebraic concepts. Minimal prerequisites. Numerous exercises. 1951 editionProvided by publisher.

Includes bibliographical references and index.

ISBN-13: 978-0-486-48220-0 (pbk.)

ISBN-10: 0-486-48220-0 (pbk.)

1. Geometry, Analytic. 2. Algebra. I. Sperner, E. (Emanuel), 1905- II. Title.

QA551.S433 2011

516.3dc22

2011000043

Manufactured in the United States by Courier Corporation
48220001
www.doverpublications.com

Schreier and Sperners justly famous Einfhrung in die Algebra und Analytische Geometrie was originally published in two volumes. Both of these volumes (with the omission of a final chapter on projective geometry) are here presented in a one-volume English translation, under the title Introduction to Modern Algebra and Matrix Theory .

It may be noted that of the present translation (Volume II, Chapter II of the original) incorporates the material of the authors book Lectures on Matrices ( Vorlesungen ber Matrizen ).

F. S. A. G.

We wish to thank Dr. F. Steinhardt for his very valuable help in the preparation of the present translation. Thanks are due, also, to Miss Zelma Ann McCormick.

M ARTIN D AVIS

M ELVIN H AUSNER

Otto Schreier had planned, a few years ago, to have his lectures on Analytic Geometry and Algebra published in book form. Death overtook him in Hamburg on June 2, 1929, before he had really begun to carry out his plan. The task of doing this fell on me, his pupil. I had at my disposal some sets of lecture notes taken at Schreiers courses, as well as a detailed (if not quite complete) syllabus of his course drawn up at one time by Otto Schreier himself. Since then, I have also given the course myself, in Hamburg, gaining experience in the process.

In writing the book I have followed Schreiers presentation as closely as possible, so that the textbook might retain the characteristics impressed on the subject matter in Otto Schreiers treatment. In particular, as regards choice and arrangement of material, I have followed Schreiers outline faithfully, except for a few changes of minor importance.

This textbook is motivated by the idea of offering the student, in two basic courses on Calculus and Analytic Geometry, all that he needs for a profitable continuation of his studies adapted to modern requirements. It is evident that this implies a stronger emphasis than has been customary on algebra, in line with the recent developments in that subject.

The prerequisites for reading this book are few indeed. For the early parts, a knowledge of the real number systemsuch as is acquired in the first few lectures of almost any calculus courseis sufficient. The later chapters make use of some few theorems on continuity of real functions and on sequences of real numbers. These also will be familiar to the student from the calculus. In some sections which give intuitive interpretations of the subject matter, use is made of some well-known theorems of elementary geometry, whose derivation on an axiomatic basis would of course be beyond the scope of this text.

What the book contains may be seen in outline by a glance at the table of contents. The student is urged not to neglect the exercises at the end of each section; among them will be found many an important addition to the material presented in the text.

To Messrs. E. Artin and W. Blaschke in Hamburg I wish to extend my most cordial thanks for their manifold help. I also wish to express my gratitude for reading the proofs, to Miss A. Voss (Hamburg) and to Messrs. R. Brauer (Koenigsberg), G. Feigl (Berlin), K. Henke (Hamburg), and E. Schubarth (Basel).

E MANUEL S PERNER

FROM THE PREFACE TO VOLUME II
OF THE GERMAN EDITION

The second volume of Einfhrung in die Analytische Geometrie und Algebra is divided into three chapters, the first two of which [ of the present translation] deal with algebraic topics, while the last, and longest, [to be published as a separate volume. Ed .] is an analytic treatment of ( n -dimensional) projective geometry.

The authors earlier monograph, Vorlesungen ber Matrizen ( Hamburger Einzelschriften , Vol. 12) has been incorporated into [ of] the present book, with a few re-arrangements and omissions in order to achieve a more organic whole.

To Mr. W. Blaschke (Hamburg) I owe a debt of gratitude for his continuous interest and help. I also wish to thank Messrs. O. Haupt (Erlangen) and K. Henke (Hamburg) for many valuable hints and suggestions. In preparing the manuscript, my wife has given me untiring assistance. For reading the proofs I am indebted to Mr. H. Bueckner (Koenigsberg), in addition to those named above.

Koenigsberg, October 1935.

E MANUEL S PERNER

C HAPTER I
AFFINE SPACE; LINEAR EQUATIONS

C HAPTER II
EUCLIDEAN SPACE; THEORY OF DETERMINANTS

C HAPTER III
FIELD THEORY; THE FUNDAMENTAL THEOREM OF ALGEBRA

C HAPTER IV
ELEMENTS OF GROUP THEORY

C HAPTER V
LINEAR TRANSFORMATIONS AND MATRICES

There is an intimate connection between the properties of lines, planes, and space and those of certain numerical structures. It is this relation which provides the foundation for analytic geometry. Our first task will be to establish it.

1. The straight line or one-dimensional space. Let us fix two distinct points O and E on the line g ( Thus a point and its abscissa determine each other uniquely. Every point of the line determines one and only one real number, and every real number determines one and only one point of the line . We also express this by saying that there is a one-to-one correspondence between the points of a line and the totality of all real numbers. If this correspondence is set up by the method described above, we shall say that a coordinate system has been introduced on the line. Observe that the coordinate system is completely determined by the choice of origin and unit point.

Fig. 1

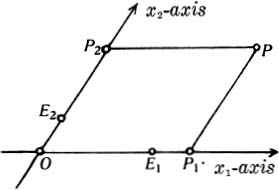
Fig. 2

We shall now assign to every point P of the plane a pair of real numbers which we call the coordinates of that point. We draw the two lines through P which are parallel respectively to the two axes. Let the one intersect the x -axis in the point P , and the other intersect the x -axis in the point P . Let x be the abscissa of the point P in the coordinate system we have introduced on the x -axis, and similarly let x be the abscissa of the point P in the coordinate system we have introduced on the x -axis. We then assign the numbers x , x to the point P as its coordinates. x is called its first coordinate and x its second . For every pair x , x of real numbers, there will be one and only one point having x as its first, and x as its second, coordinate. For, let P be that point on the x -axis which has x as its abscissa on this axis, and let P be that point on the x -axis which has x as its abscissa on the x -axis. The line through P parallel to the x -axis and the line through P parallel to the x -axis will meet at a point P . P will then have x and x as its first and second coordinates respectively, and is obviously the only such point.