A.I. Introduction
A.11. Recently the concept of a category and certain related ideas have begun to play an important role in various branches of mathematics. An example of a category is a collection of sets together with mappings of the sets into one another. A collection of linear spaces or algebras together with their morphisms is another example of a category.
The exact definition of a category is as follows: Let 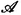 be a set of indices , and let
be a set of indices , and let 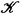 be a set of elements X (
be a set of elements X ( 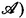 called objects of the category
called objects of the category 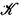 . Suppose that for every pair of objects X , and X there is a set
. Suppose that for every pair of objects X , and X there is a set  of other elements A called mappings of the object X into the object X such that the product of the mappings A and A is defined for arbitrary , , and belongs to
of other elements A called mappings of the object X into the object X such that the product of the mappings A and A is defined for arbitrary , , and belongs to  , where multiplication is associative, i.e.,
, where multiplication is associative, i.e.,
A ( A A ) = ( A A ) A )
for arbitrary , , , . ln particular, the set  of mappings of the objects X into themselves is defined, and (associative) multiplication of mappings is defined in
of mappings of the objects X into themselves is defined, and (associative) multiplication of mappings is defined in  . Finally, it is required that the set
. Finally, it is required that the set  contain the unit element , which has the property that
contain the unit element , which has the property that
A = A , A = A
for arbitrary , and . Instead of  we will usually write simply
we will usually write simply  .
.
A set 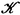 of objects X and mappings A with the properties just enumerated is called a category. A category
of objects X and mappings A with the properties just enumerated is called a category. A category 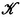 is called linear if in the set
is called linear if in the set  of mappings A (with arbitrary fixed and ) there are defined operations of addition of mappings and multiplication of mappings by numbers (from the field K). This makes the set
of mappings A (with arbitrary fixed and ) there are defined operations of addition of mappings and multiplication of mappings by numbers (from the field K). This makes the set  into a linear space over the field K. Thus in a linear category the set
into a linear space over the field K. Thus in a linear category the set  becomes an algebra with a unit (over the field K ).
becomes an algebra with a unit (over the field K ).
A.12 . In this appendix we will consider linear categories whose elements are finite-dimensional linear spaces (of dimension 1) over the field C of complex numbers, while the mappings are linear mappings (morphisms) of one such space into another.
Thus we start with the following definition: Let X ( 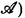 be a set of finite-dimensional complex linear spaces, and for every let
be a set of finite-dimensional complex linear spaces, and for every let  be an algebra of linear operators carrying X into itself. Moreover, suppose that for every pair of indices and there is a set
be an algebra of linear operators carrying X into itself. Moreover, suppose that for every pair of indices and there is a set  of linear operators A carrying X into X such that I) if
of linear operators A carrying X into X such that I) if  contains the operators A and B , then
contains the operators A and B , then  contains the operator sum A + B , and 2) if
contains the operator sum A + B , and 2) if  contains the operator A , then
contains the operator A , then  contains the product A where is an arbitrary complex number. A family of linear operators with these two properties will be called a linear family. In particular, the linear family
contains the product A where is an arbitrary complex number. A family of linear operators with these two properties will be called a linear family. In particular, the linear family  coincides with the algebra
coincides with the algebra  . It is also assumed that
. It is also assumed that
for arbitrary , and , i.e., that every product
A A ( A  , A
, A 
 )
)
belongs to  . Such a set of spaces X together with algebras
. Such a set of spaces X together with algebras  and linear families
and linear families  will be called a category of finite-dimensional spaces or simply a category , and will be denoted by
will be called a category of finite-dimensional spaces or simply a category , and will be denoted by  .
.
If we choose a basis in every space X, then the algebras  and linear families
and linear families  can be identified with the algebras and linear families of the corresponding matrices, a fact which will henceforth be exploited systematically.
can be identified with the algebras and linear families of the corresponding matrices, a fact which will henceforth be exploited systematically.
In what follows, we will find the categories of linear spaces corresponding to given algebras  , confining ourselves to the case where the
, confining ourselves to the case where the  are semisimple algebras containing the unit matrix. According to Sec. 11.86, for such an algebra the space X can be decomposed into a direct sum of subspaces X, invariant under all the operators A, where in each subspace Xj the algebra
are semisimple algebras containing the unit matrix. According to Sec. 11.86, for such an algebra the space X can be decomposed into a direct sum of subspaces X, invariant under all the operators A, where in each subspace Xj the algebra  is a simple algebra containing the unit matrix, i.e., is described in some basis by the set of all quasi-diagonal matrices of the form
is a simple algebra containing the unit matrix, i.e., is described in some basis by the set of all quasi-diagonal matrices of the form












 be a set of indices , and let
be a set of indices , and let  be a set of elements X (
be a set of elements X ( 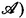 called objects of the category
called objects of the category 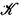 . Suppose that for every pair of objects X , and X there is a set
. Suppose that for every pair of objects X , and X there is a set  of other elements A called mappings of the object X into the object X such that the product of the mappings A and A is defined for arbitrary , , and belongs to
of other elements A called mappings of the object X into the object X such that the product of the mappings A and A is defined for arbitrary , , and belongs to 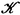 of objects X and mappings A with the properties just enumerated is called a category. A category
of objects X and mappings A with the properties just enumerated is called a category. A category 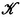 is called linear if in the set
is called linear if in the set 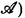 be a set of finite-dimensional complex linear spaces, and for every let
be a set of finite-dimensional complex linear spaces, and for every let 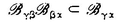
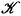 .
.