Georgi E. Shilov - Elementary Real and Complex Analysis
Here you can read online Georgi E. Shilov - Elementary Real and Complex Analysis full text of the book (entire story) in english for free. Download pdf and epub, get meaning, cover and reviews about this ebook. year: 1996, publisher: Dover Publications, genre: Children. Description of the work, (preface) as well as reviews are available. Best literature library LitArk.com created for fans of good reading and offers a wide selection of genres:
Romance novel
Science fiction
Adventure
Detective
Science
History
Home and family
Prose
Art
Politics
Computer
Non-fiction
Religion
Business
Children
Humor
Choose a favorite category and find really read worthwhile books. Enjoy immersion in the world of imagination, feel the emotions of the characters or learn something new for yourself, make an fascinating discovery.
- Book:Elementary Real and Complex Analysis
- Author:
- Publisher:Dover Publications
- Genre:
- Year:1996
- Rating:5 / 5
- Favourites:Add to favourites
- Your mark:
Elementary Real and Complex Analysis: summary, description and annotation
We offer to read an annotation, description, summary or preface (depends on what the author of the book "Elementary Real and Complex Analysis" wrote himself). If you haven't found the necessary information about the book — write in the comments, we will try to find it.
In this book the renowned Russian mathematician Georgi E. Shilov brings his unique perspective to real and complex analysis, an area of perennial interest in mathematics. Although there are many books available on the topic, the present work is specially designed for undergraduates in mathematics, science and engineering. A high level of mathematical sophistication is not required.
The book begins with a systematic study of real numbers, understood to be a set of objects satisfying certain definite axioms. The concepts of a mathematical structure and an isomorphism are introduced in Chapter 2, after a brief digression on set theory, and a proof of the uniqueness of the structure of real numbers is given as an illustration. Two other structures are then introduced, namely n-dimensional space and the field of complex numbers.
After a detailed treatment of metric spaces in Chapter 3, a general theory of limits is developed in Chapter 4. Chapter 5 treats some theorems on continuous numerical functions on the real line, and then considers the use of functional equations to introduce the logarithm and the trigonometric functions. Chapter 6 is on infinite series, dealing not only with numerical series but also with series whose terms are vectors and functions (including power series). Chapters 7 and 8 treat differential calculus proper, with Taylors series leading to a natural extension of real analysis into the complex domain. Chapter 9 presents the general theory of Riemann integration, together with a number of its applications. Analytic functions are covered in Chapter 10, while Chapter 11 is devoted to improper integrals, and makes full use of the technique of analytic functions.
Each chapter includes a set of problems, with selected hints and answers at the end of the book. A wealth of examples and applications can be found throughout the text. Over 340 theorems are fully proved.
Georgi E. Shilov: author's other books
Who wrote Elementary Real and Complex Analysis? Find out the surname, the name of the author of the book and a list of all author's works by series.











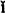 Evgenevich) [Matematicheski
Evgenevich) [Matematicheski 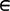 A (or A
A (or A 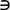 a) we mean that a is an element of the set A, while by a
a) we mean that a is an element of the set A, while by a 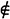 A (or a
A (or a 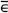 A) we mean that a is not an element of the set A. By A
A) we mean that a is not an element of the set A. By A B (or B
B (or B A) we mean that every element of the set A is an element of the set
A) we mean that every element of the set A is an element of the set