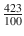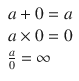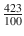Natasha Maurits - Math for Scientists: Refreshing the Essentials
Here you can read online Natasha Maurits - Math for Scientists: Refreshing the Essentials full text of the book (entire story) in english for free. Download pdf and epub, get meaning, cover and reviews about this ebook. year: 2017, publisher: Springer International Publishing, genre: Children. Description of the work, (preface) as well as reviews are available. Best literature library LitArk.com created for fans of good reading and offers a wide selection of genres:
Romance novel
Science fiction
Adventure
Detective
Science
History
Home and family
Prose
Art
Politics
Computer
Non-fiction
Religion
Business
Children
Humor
Choose a favorite category and find really read worthwhile books. Enjoy immersion in the world of imagination, feel the emotions of the characters or learn something new for yourself, make an fascinating discovery.
- Book:Math for Scientists: Refreshing the Essentials
- Author:
- Publisher:Springer International Publishing
- Genre:
- Year:2017
- Rating:4 / 5
- Favourites:Add to favourites
- Your mark:
Math for Scientists: Refreshing the Essentials: summary, description and annotation
We offer to read an annotation, description, summary or preface (depends on what the author of the book "Math for Scientists: Refreshing the Essentials" wrote himself). If you haven't found the necessary information about the book — write in the comments, we will try to find it.
This book reviews math topics relevant to non-mathematics students and scientists, but which they may not have seen or studied for a while. These math issues can range from reading mathematical symbols, to using complex numbers, dealing with equations involved in calculating medication equivalents, the General Linear Model (GLM) used in e.g. neuroimaging analysis, finding the minimum of a function, independent component analysis, or filtering approaches. Almost every student or scientist, will at some point run into mathematical formulas or ideas in scientific papers that may be hard to understand, given that formal math education may be some years ago.In this book we will explain the theory behind many of these mathematical ideas and expressions and provide readers with the tools to better understand them. We will revisit high school mathematics and extend and relate this to the mathematics you need to understand the math you may encounter in the course of your research. This book will help you understand the math and formulas in the scientific papers you read. To achieve this goal, each chapter mixes theory with practical pen-and-paper exercises such that you (re)gain experience with solving math problems yourself. Mnemonics will be taught whenever possible. To clarify the math and help readers apply it, each chapter provides real-world and scientific examples.
Natasha Maurits: author's other books
Who wrote Math for Scientists: Refreshing the Essentials? Find out the surname, the name of the author of the book and a list of all author's works by series.
Natasha Maurits
Arthur Benjamin
Ian Stewart
Jeffrey Bennett
Theoni Pappas
Math for Scientists: Refreshing the Essentials — read online for free the complete book (whole text) full work
Below is the text of the book, divided by pages. System saving the place of the last page read, allows you to conveniently read the book "Math for Scientists: Refreshing the Essentials" online for free, without having to search again every time where you left off. Put a bookmark, and you can go to the page where you finished reading at any time.
Light
Font size:
↓
↑
Reset
Interval:
↓
↑
Bookmark:
Make
Springer International Publishing AG 2017
Natasha Maurits and Branislava uri-Blake Math for Scientists1. Numbers and Mathematical Symbols
Natasha Maurits 1
(1)
Department of Neurology, University Medical Center Groningen, Groningen, The Netherlands
Natasha Maurits
Email:
After reading this chapter you know:
- what numbers are and why they are used,
- what number classes are and how they are related to each other,
- what numeral systems are,
- the metric prefixes,
- how to do arithmetic with fractions,
- what complex numbers are, how they can be represented and how to do arithmetic with them,
- the most common mathematical symbols and
- how to get an understanding of mathematical formulas.
1.1 What Are Numbers and Mathematical Symbols and Why Are They Used?
A refresher course on mathematics can not start without an introduction to numbers. Firstly, because one of the first study topics for mathematicians were numbers and secondly, because mathematics becomes really hard without a thorough understanding of numbers. The branch of mathematics that studies numbers is called number theory and arithmetic forms a part of that. We have all learned arithmetic starting from kindergarten throughout primary school and beyond. This suggests that an introduction to numbers is not even necessary; we use numbers on a day-to-day basis when we count and measure and you might think that numbers hold no mysteries for you. Yet, arithmetic can be as difficult to learn as reading and some people never master it, leading to dyscalculia .
So, what is a number? You might say: well, five is a number and 243, as well as 1963443295765. This is all true, but what is the essence of a number? You can think of a number as an abstract representation of a quantity that we can use to measure and count. It is represented by a symbol or numeral, e.g., the number five can be represented by the Arabic numeral 5, by the Roman numeral V, by five fingers, by five dots on a dice, by |||| , by five abstract symbols such as and in many other different ways. Synesthetes even associate numbers with colors. But, importantly, independent of how a number is represented, the abstract notion of this number does not change.
Most likely, (abstract) numbers were introduced after people had developed a need to count. Counting can be done without numbers, by using fingers, sticks or pebbles to represent single or groups of objects. It allows keeping track of stock and simple communication, but when quantities become larger, this becomes more difficult, even when abstract words for small quantities are available. A more compact way of counting is to put a marklike a scratch or a lineon a stick or a rock for each counted object. We still use this approach when tally marking. However, marking does not allow dealing with large numbers either. Also, these methods do not allow dealing with negative numbers (as e.g., encountered as debts in accounting), fractions (to indicate a part of a whole) or other even more complex types of numbers.
The reason that we can deal with these more abstract types of numbers, that no longer relate to countable series of objects, is that numeral systems have developed over centuries. In a numeral system a systematic method is used to create number words, so that it is not necessary to remember separate words for all numbers, which would be sheer impossible. Depending on the base that is used, this systematic system differs between languages and cultures. In many current languages and cultures base 10 is used for the numeral system, probably as a result of initially using the 10 digits (fingers and thumbs) to count. In this system, enumeration and numbering is done by tens, hundreds, thousands etcetera. But remnants of older counting systems are still visible, e.g. in the words twelve (which is not ten-two) or quatre-vingts (80 in French; four twenties). For a very interesting, easy to read and thorough treatise on numbers please see Posamenter and Thaller ().
We now introduce the first mathematical symbols in this book; for numbers. In the base 10 numeral system the Arabic numerals 0, 1, 2, 3, 4, 5, 6, 7, 8 and 9 are used. In general, mathematical symbols are useful because they help communicating about abstract mathematical structures, and allow presenting such structures in a concise way. In addition, the use of symbols speeds up doing mathematics and communicating about it considerably, also because every symbol in its context only has one single meaning. Interestingly, mathematical symbols do not differ between languages and thus provide a universal language of mathematics. For non-mathematicians, the abstract symbols can pose a problem though, because it is not easy to remember their meaning if they are not used on a daily basis. Later in this chapter, we will therefore introduce and explain often used mathematical symbols and some conventions in writing mathematics. In this and the next chapters, we will also introduce symbols that are specific to the topic discussed in each chapter. They will be summarized at the end of each chapter.
1.2 Classes of Numbers
When you learn to count, you often do so by enumerating a set of objects. There are numerous children (picture) books aiding in this process by showing one ball, two socks, three dolls, four cars etcetera. The first numbers we encounter are thus 1, 2, 3, Note that is a mathematical symbol that indicates that the pattern continues. Next comes zero. This is a rather peculiar number, because it is a number that signifies the absence of something. It also has its own few rules regarding arithmetic: 
Here, a is any number and is the symbol for infinity, the number that is larger than any countable number.
Together, 0, 1, 2, 3, are referred to as the natural numbers with the symbol . A special class of natural numbers is formed by the prime numbers or primes; natural numbers >1 that only have 1 and themselves as positive divisors. The first prime numbers are 2, 3, 5, 7, 11, 13, 17, 19 etcetera. An important application of prime numbers is in cryptography , where they make use of the fact that it is very difficult to factor very large numbers into their primes. Because of their use for cryptography and because prime numbers become rarer as numbers get larger, special computer algorithms are nowadays used to find previously unknown primes.
The basis set of natural numbers can be extended to include negative numbers: , 3, 2, 1, 0, 1, 2, 3, Negative numbers arise when larger numbers are subtracted from smaller numbers, as happens e.g. in accounting, or when indicating freezing temperatures indicated in C (degrees Centigrade). These numbers are referred to as the integer numbers with symbol (for zahl, the German word for number). Thus is a subset of .
By dividing integer numbers by each other or taking their ratio, we get fractions or rational numbers, which are symbolized by (for quotient). Any rational number can be written as a fraction, i.e. a ratio of an integer, the numerator , and a positive integer, the denominator . As any integer can be written as a fraction, namely the integer itself divided by 1, is a subset of . Arithmetic with fractions is difficult to learn for many; to refresh your memory the main rules are therefore repeated in Sect..
Numbers that can be measured but that can not (always) be expressed as fractions are referred to as real numbers with the symbol . Real numbers are typically represented by decimal numbers, in which the decimal point separates the ones digit from the tenths digit (see also Sect. on numeral systems) as in 4.23 which is equal to 
Light
Font size:
↓
↑
Reset
Interval:
↓
↑
Bookmark:
Make
Similar books «Math for Scientists: Refreshing the Essentials»
Look at similar books to Math for Scientists: Refreshing the Essentials. We have selected literature similar in name and meaning in the hope of providing readers with more options to find new, interesting, not yet read works.
Arthur Benjamin
Ian Stewart
Jeffrey Bennett
Theoni Pappas
Reviews about «Math for Scientists: Refreshing the Essentials»
Discussion, reviews of the book Math for Scientists: Refreshing the Essentials and just readers' own opinions. Leave your comments, write what you think about the work, its meaning or the main characters. Specify what exactly you liked and what you didn't like, and why you think so.