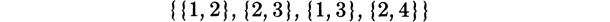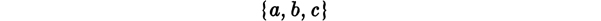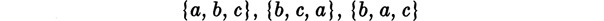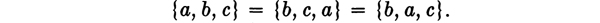J. B. Roberts - The Real Number System in an Algebraic Setting

J. B. Roberts

Reed College

Dover Publications, Inc.

Mineola, New York

Bibliographical Note

This Dover edition, first published in 2018, is an unabridged republication of the work originally published in 1962 by W. H. Freeman and Company, San Francisco and London.

Library of Congress Cataloging-in-Publication Data

Names: Roberts, Joe, author.

Title: The real number system in an algebraic setting / J.B. Roberts.

Description: Dover edition. | Mineola, New York : Dover Publications, Inc., 2018. | Originally published: San Francisco : W.H. Freeman, 1962. | Includes bibliographical references.

Identifiers: LCCN 2017046607| ISBN 9780486824512 | ISBN 0486824519

Subjects: LCSH: ArithmeticFoundations. | Number theory. | Numbers, Real.

Classification: LCC QA255 .R64 2018 | DDC 512.7/86dc23

LC record available at https://lccn.loc.gov/2017046607

Manufactured in the United States by LSC Communications

82451901 2018

www.doverpublications.com

T HIS course of study is intended to acquaint the student with the basic facts of a mathematical system of great importance. The course, while being quite detailed and technical, is of great cultural value to nonscience students. It seems that one cannot have any real understanding of what mathematics is about, what its methods are, and what is meant by mathematical creativity without having detailed experience in some technical aspect of mathematics.

Because of its beauty and intrinsic interest, as well as its complexity, the real number system is an excellent vehicle for conveying to the beginner the power and precision of a mathematical system. A wealth of methods, ideas, and techniques is necessarily placed in the forefront.

In this course I have tried to use those methods which will be of greatest importance in future work. Many important ideas from algebra are introduced early. At the same time I have tried to presuppose nothing more than that the student be familiar with the basic properties of the natural numbers and that he be willing to think hard about the subject. is devoted to a discussion of the mathematics assumed. The text itself is not complete. Many gaps are left to be filled by completing the exercises; thus many of the exercises must be regarded as part of the text. These are marked with an asterisk. The student should certainly work all of these and in general should work every exercise.

No proofs are given in the first section of this task on his own or for an outside examination. Treated in this way, much of the course becomes integrated in the students mind. More important, he gains confidence in his ability to carry out a complicated bit of reasoning.

It is almost inevitable that sometime during the course there will be questions about infinite sets and infinite cardinal numbers. To satisfy the students needs, two appendixes introduce these notions. These appendixes are not necessary to the main development and may be omitted from it. Also included as an appendix is a short introduction to the complex numbers.

This book is the outgrowth of a set of notes that have undergone almost continuous transformation since they were first written in 1956-1957. During each of the past five years I have used them in my classes, and during the past four years several of my colleagues at Reed College have used them. I do not delude myself into thinking that the material cannot be further improved and would welcome any suggestions.

July 1961

J. B. Roberts

When we speak of a collection in mathematics we intend roughly the same meaning as when the word is used in everyday language. Thus, if we are considering the first five natural numbers denoted by 1, 2, 3, 4, 5, we speak of the collection {1, 2, 3, 4, 5}; the names of the individual elements (or members) of the collection are enclosed in brackets.

The collection {, *, } has three elements whose names are , *, and . There are many other collections such as:

(1) The collection Z of all natural numbers: {1, 2, 3,}. (Here the three dots indicate that the string of numbers in the collection continues in a similar way indefinitely.)

(2) The collection of all even natural numbers: {2, 4, 6, }.

(3) The collection of all natural numbers less than or equal to 20 : {1, 2, 3,, 20}. (Here the three dots indicate that the string of numbers in the collection continues in a similar way until 20 is reached, at which place the string stops.)

(4) The collection of all living people. (We do not try to use the bracket notation in a case such as this.)

(5) The collection of Reed College freshman girls.

(6) The collection of all living centaurs. (This collection has no members and is therefore referred to as the empty set. It may seem strange to speak of such a set, but we shall see later that it is a very useful concept. We consider the set of all living centaurs to be the same as the set of all men over 20 feet tall; that is, there is only one empty set. The empty set is denoted by .)

Note that a collection cannot contain a given element more than once.

Several words are used synonymously with the word collection. In this text we shall use set and class. Thus, the collection {1, 2} will often be called the set {1, 2} or the class {1, 2}.

If each element of one set A is an element of a second set B, then we call the set A a subset of the set B. In particular, both B and are subsets of B. The subsets of the set {a, b, c} are , {a} {b}, {c}, {a, b}, {a, c}, {b, c}, and {a, b, c}.

A proper subset of a set is any subset other than the empty set and the set itself. Thus, the proper subsets of {a, b, c} are all those subsets listed above except the first and the last.

Quite often the collections we wish to consider have as elements not single members or objects, as in the above examples, but sets of objects. For instance, the collection

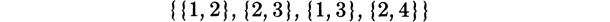
has as elements the sets {1, 2}, {2, 3}, {1, 3}, and {2, 4}. Thus, this is a set of sets (or a collection of sets).

When we write

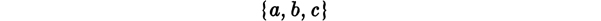
we are dealing with a collection containing as elements the objects denoted by a, b, and c. These objects are not ordered in any special way of course we must write their names in some order, but the order is not to be regarded as being of any significance. In this light, all of the expressions

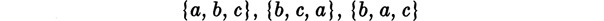
are names for the same collection and we write

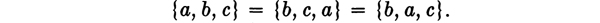
In general, two sets are equal if and only if they have exactly the same elements.