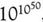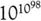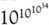I would like to thank the staff at W. H. Freeman and Company for their help in producing this book, especially my editor John Michel, who made significant contributions to the form of the book; Nancy Brooks, whose copyediting transcended copyediting; and Jane ONeill, who shepherded a difficult production task and schedule. I also want to thank my wife, Mary, for her contributions as first reader and aid in indexing and for overseeing the author.
The following books contain additional information on numbers, mental computation, and infinity.
Numbers
Clawson, Calvin C. Mathematical Mysteries: The Beauty and Magic of Numbers . New York, Plenum Press, 1996.
Conway, John H., and Richard K. Guy. The Book of Numbers. New York, Copernicus (Springer-Verlag), 1996.
Dehaene, Stanislas. The Number Sense. New York, Oxford University Press, 1997.
Guedj, Denis (tr. by Lory Frankel). Numbers: The Universal Language. New York, Harry N. Abrams, Inc. 1997.
Menninger, Karl (tr. by Paul Broneer). Number Words and Number Symbols: A Cultural History of Numbers . New York, Dover, 1992.
Ore, Oystein. Number Theory and Its History. New York, Dover Publications, 1988.
Phillips, Richard. Numbers: Facts, Figures, and Fiction . Cambridge, MA, Cambridge University Press, 1995.
Wells, David G. The Penguin Dictionary of Curious and Interesting Numbers . New York, Penguin USA, 1998.
Mental Computation
Julius, Edward H. Arithmetricks: 50 Easy Ways to Add, Subtract, Multiply, and Divide Without a Calculator. New York, John Wiley & Sons, 1995.
Infinity
Lavine, Shaughan. Understanding the Infinite . Cambridge, MA, Harvard University Press, 1998.
Morris, Richard. Achilles in the Quantum Universe: The Definitive History of Infinity. New York, Henry Holt & Company, 1997.
Pickover, Clifford A. Keys to Infinity. New York, John Wiley & Sons, 1997.
Numbers with interesting properties discussed in this Field Guide are indexed below in the order of their absolute values; when absolute values are the same, positive numbers are listed first, followed by negatives and complex numbers.
1/47
1/42
1/37
-1/30
1/27
1/16
5/66
1/10
0.1100010000000000000000010
1/9
1/8
1/7
1/6
1/5
1/4
691/2730
1/3
2/5
1/2
0.61803398 (1/)
2/3
-1
i
ei
7/6
1.414213562373 (2)
1 + i
1.61803398 ()
1.732 (3)
-2
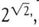
p.
2.718281828459045 (e)
-3
3.14
3.14159265358979 ()
22/7
-7
3617/510
-11
-19
-43
-67
-163
625,p.3
1000
1001
1024
1184
1200
1210
1225
1331
1430
1728
1729
1776
2047
21977 p.
2620
2744
2924
3375
4096
4862
4913
5040
5832
6859
7560
8000
8128
8191
9240
16,796
17,296
17,389
18,416
35,645
41,616
59,049
65,537
131,071
142,857
368,640
524,287
1,000,000
1,413,721
1,701,936
3,492,725
9,363,584
9,437,056
2,229,530,000
6,000,000,000
6,000,000,000,000
8,813,200,023,188
1,111,111,111,111,111,111
11,111,111,111,111,111,111,111
2 127 - 1
1063
1076
1096
10100,pp. 177, 179-180
26,972,593 -1
102,400,000,000
10googol
In some societies, counting language has not evolved beyond 2 or 3 and a word that means many for higher numbers. From a linguistic point of view the counting numbers, at least those greater than 2 or 3, may be considered a human invention.
Yet there is something natural about the genus Natural. If the concept of matching, or one-to-one correspondence, is taken as a fundamental idea, the natural numbers1, 2, 3, would appear to be its logical outgrowth; a natural number describes the set of all sets that can be matched a member at a time with a given set, without regard to order.
From this point of view, 1 might be considered the characteristic that all the sets which match with me myself, considered as an individual, have in common. The number 2 is characteristic of collections that match my eyes or hands or legs or ears. Then 3 is part of the description of sets that match the spaces between the knuckles on one hand, 4 the sets that match the fingers without the thumb, 5 with the thumb, and so forth. You see why some societies stopped using natural numbers after 2 or 3, since we quickly begin to exhaust the observables shared by all.
Although the idea of one-to-one correspondence may seem naturalit is pretty much what we teach to young children as the meaning of numberit is not very mathematical as most mathematicians for the past 200 years haveenvisioned the field. Mathematical ideas must be pinned down; it is not enough to say that we abstract a concept from experience. The definition of a mathematical entity must be operationalthat is, there must be some operation that produces the entity. Furthermore, the operation needs to emerge from within mathematics. The ancient Greeks were satisfied, for example, with the idea that geometric figures are congruent if one may be picked up and superimposed on another. This intuitive idea is rejected today because superimposition is not a mathematical operation. Congruence is established instead with a series of definitions based on such ideas as equality of lengths or angles, which are part of mathematics generally. So it is with the numbersinstead of the natural interpretation of numbers, mathematicians use the counting interpretation. The nineteenth-century German mathematician Richard Dedekind, the first to define the genus Real without recourse to geometry, wrote: I regard the whole of arithmetic as a necessary, or at least natural, consequence of the simplest arithmetic act, that of counting.
Several mathematical definitions based on counting have been proposed for genus Natural. The most common and in some ways the most acceptable was developed by the Italian mathematician Giuseppe Peano [1858-1932] in 1889. It combines the idea of counting with a very general principle called mathematical induction that applies nicely to counting numbers. The Peano definition is a set of five axioms that begins simply and becomes increasingly less intuitive, but still manages to have the axiomatic property of seeming inevitable (although a certain amount of reflection is required to grasp the essence of the last two). Those who are familiar with Euclids five postulates for geometry will notice a certain parallel.














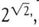 p.
p.