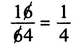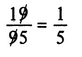Bryan Bunch - Mathematical Fallacies and Paradoxes

One should not forget that the functions, like all mathematical constructions, are only our own creations, and that when the definition with which one begins ceases to make sense, one should not ask, What is, but what is convenient to assume in order that it remains significant.

Karl Friedrich Gauss

Everybody makes mistakes. In particular, everybody makes mistakes in mathematics. Everybody includes mathematicians, even some of the greatest of all time.

If you add two numbers and get a wrong sum, the mistake is just a mistake. If the wrong answer results from an argument that seems to make it correct, the mistake is a fallacy. Sometimes students give explanations for mistakes that sound very logical. But the sum is still wrong.

Here is a very simple example of such a mistake. This one is made deliberately. You may have seen the following trick played on a child (or even on an unsuspecting adult). You go to the child and say that you can prove that he or she has 11 fingers. How? says the child, who knows perfectly well that almost everyone has 10 fingers. By counting.

You proceed to count the fingers in the ordinary way, laying one of your fingers on each one of the childs in turn.

1, 2, 3, 4, 5, 6, 7, 8, 9, 10

Oh, you say, I must have made a mistake. Let me do it the other way. Starting with the little finger you count backwards:

10, 9, 8, 7, 6

You are now at the thumb. You stop and say, And 5 more from the other hand, which we counted before, makes 11.

An incorrect result coupled with an apparently logical explanation of why the result is correct is a fallacy . (The word fallacy is also used to refer to incorrect beliefs in general, but in mathematics the incorrect chain of reasoning is essential to the situation.) In fact, the word in mathematical usage could also refer to a correct result obtained by incorrect reasoning, as, for example, the student who used cancellation for reducing fractions as follows:

and

The student got the correct result in these cases, but the method has no logical basis and generally would fail.

Sometimes the mistakes in reasoning come because your experience with one situation causes you to assume that the same reasoning will hold true in a related but different situation. This mistake can happen at a very simple level or at a more complex one. At a simple level, the most common conclusion is that you know you have to reject the reasoning, although it may be difficult to say why. At the more complex level, you may conclude that the reasoning must be accepted even when the results seem to contradict your notion of how the real world works.

No one is quite sure why reasoning and mathematics so often seem to explain the real world. Experience has shown, however, that when the results of reasoning and mathematics conflict with experience in the real world, there is probably a fallacy of some sort involved. As long as you do not know what the fallacy is, the situation is a paradox . In some cases, as you will see, the paradox is entirely within mathematics. In others, it is in language or in events in the real world (with associated reasoning). For most paradoxes that are within mathematics, elimination of the fallacious reasoning produces a purified mathematics that is a better description of the real world than the impure mathematics was. So be it.

In looking at wrong thinking about easy ideas, you will find some cases in which reasoning about the real world is wrong because of a lack of experience with parts of the real world. In other cases, reasoning about mathematics is wrong because certain operations must be ruled out of mathematics. There are also situations in which reasoning is not the right approach to take to the real world.