Haim Shapira was born in Lithuania in 1962. In 1977 he emigrated to Israel, where he earned a PhD in mathematical genetics for his dissertation on Game Theory and another PhD for his research on the mathematical and philosophical approaches to infinity. He now teaches mathematics, psychology, philosophy and literature. He is an author of nine bestselling books. His stated mission as a writer is not to try to make his readers agree with him, but simply to encourage them to enjoy thinking. One of Israels most popular and sought-after speakers, he lectures on creativity and strategic thinking, existential philosophy and philosophy in childrens literature, happiness and optimism, nonsense and insanity, imagination and the meaning of meaning, as well as friendship and love. He is also an accomplished pianist and an avid collector of anything beautiful.
BY THE SAME AUTHOR:
Conversations on Game Theory
Things That Matter
The Wisdom of King Solomon: A Contemporary Exploration of Ecclesiastes and the Meaning of Life
Gladiators, Pirates and Games of Trust: How Game Theory,
Strategy and Probability Rule Our Lives
Nocturnal Musings
A Book of Love
Happiness and Other Small Things of Absolute Importance
A Most Beautiful Childhood Memory
Contents
Acknowledgements
Introduction
Warm-up A short introduction to thinking
Lesson 1 The wonderful world of numbers Pythagoras
Lesson 2 Ramanujan and Pythagorass pebbles
Part 1: A man who knew infinity
Part 2: Pythagoras on the beach
Lesson 3 The secret lives of prime numbers
Lesson 4 Pythagorass great discovery
Lesson 5 The tortoise, Achilles and the arrow Zenos paradoxes
Lesson 6 Georg Cantors kingdom of infinity set theory
Lesson 7 Hilberts grand hotel Infinity
Lesson 8 Cardinals and the taming of the infinite
Conclusion
Notes
Further reading
ACKNOWLEDGEMENTS
First and foremost, I would like to thank Etan Ilfeld for having confidence in me and my books.
Id like to acknowledge with gratitude my faithful translator Linda Yechiel.
I would like to express my special thanks to Alain Dekker, who never stopped challenging me, for his enormous help and patience.
To Tom Benhamou, a set theory expert, who wisely edited my book and is responsible for many great insights a very big thank you.
I would like also to thank the books project manager, Slav Todorov, and to express my appreciation for everyone at Watkins who laboured over this book.
Last but never least, I would like to thank my agents, Vicki Satlow and Ziv Lewis.
INTRODUCTION
If I were again beginning my studies, I would follow the advice of Plato and start with mathematics.
(Galileo Galilei)
The English biologist and public intellectual Richard Dawkins once noted that no one is ever proud to admit that he or she is a boor and an ignoramus with respect to literature, but it is socially acceptable to proudly admit total illiteracy when it comes to science, with the epitome being perfect illiteracy with respect to mathematics. Dawkins was not the first to note this he himself points out that this concept has long become a clich.
It is very true, of course. No one would ever boast that they have never read a book, never seen a work of art, or never not even once been moved by a piece of music. If we were to conduct a survey, I am pretty sure we would discover that no educated adult has never heard of Shakespeare, Rembrandt, or Bach. They also probably recognize the names of the great mathematicians Pythagoras, Isaac Newton, and Albert Einstein. But how many have heard of Leonhard Euler or Srinivasa Ramanujan or Georg Cantor?
Perhaps, at this very moment, you are also asking yourself, What? Who are these people? Those names are unfamiliar to me.
These people are great mathematicians. Very great mathematicians!
I am a serious music, literature and art enthusiast, but I honestly believe that Ramanujans mathematical formulas are no less marvellous than Bachs musical structures, and that Cantors discoveries about infinity are as wondrous to me as Shakespeares works.
And if were already comparing cultural genius with mathematical genius, I would like to point out that Cantor was an expert on Shakespeare, and Einstein was an accomplished pianist and violinist. This is a very common phenomenon, and I know of many mathematicians who are extremely knowledgeable in literature, art, and music. In fact, German mathematician Karl Weierstrass once said that a mathematician who is not a bit of a poet will never be a good mathematician. Yet, it seems the road does not go both ways: not a few people from the field of literature, music, or the arts seem to have an aversion to mathematics.
Why is this so? Why do so many people, as educated as they may be, shy away from the intricacies and beauty yes beauty that can be found in the world of numbers and in their relationships one to the other?
Perhaps the main reason for this is mathematics inapproachability and the difficulties it places before those who wish to know her. It is true that mathematics is quite complicated, and one needs to devote time and thought to understanding its intricacies, but sometimes one has to dive to the deepest depths to find an especially exquisite pearl.
The idea to write this book came to me one day as I was perusing my collection of books on mathematics. I noticed that the majority of my books fell into one of two categories:
1 Mathematics books written for the lay audience. Some of these are wonderful books, but they focused on stories about mathematics and not on the mathematics itself.
2 Mathematics books written for mathematicians. In this category, too, are many excellent books, but only mathematicians are able to read (and understand) them.
So, I decided to write a book that would be a third category. I wanted to introduce to a lay audience, simply and clearly, two mathematical theories that I consider the most intriguing number theory and set theory, both dealing with infinity. Alongside, I would offer some strategies in mathematical thinking that would allow the reader to test his ability in solving some truly fascinating mathematical problems.
It is important to me that anybody who is curious and likes to put on a thinking cap once in a while will enjoy this book, so I restricted myself from using any fearsome mathematical symbols (you wont find any 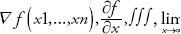 anywhere in this book). Only the most basic mathematical operations will be used (addition, subtraction, multiplication, and division, plus a couple of more advanced terms such as powers and roots), but that does not mean that you wont be required to engage in some deep thinking. I also did my best to keep the text light and give it an amusing lilt nobody really likes questions about three ducks who are filling a pool while two ducks (for reasons known only to them) are simultaneously trying to empty it.
anywhere in this book). Only the most basic mathematical operations will be used (addition, subtraction, multiplication, and division, plus a couple of more advanced terms such as powers and roots), but that does not mean that you wont be required to engage in some deep thinking. I also did my best to keep the text light and give it an amusing lilt nobody really likes questions about three ducks who are filling a pool while two ducks (for reasons known only to them) are simultaneously trying to empty it.
Comments on the book, solutions to the questions, and questions about the questions can be sent to . Wishing you a fascinating journey.
WARM-UP
A SHORT
INTRODUCTION TO THINKING
Thinking: the talking of the soul with itself.
(Plato)
If you bothered to read the introduction above (why is it that so many people never bother reading introductions?), you already know that I have a sizeable collection of mathematics books. One of my favourite occupations is to mess around with interesting problems. Well, naturally,
Next page














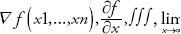 anywhere in this book). Only the most basic mathematical operations will be used (addition, subtraction, multiplication, and division, plus a couple of more advanced terms such as powers and roots), but that does not mean that you wont be required to engage in some deep thinking. I also did my best to keep the text light and give it an amusing lilt nobody really likes questions about three ducks who are filling a pool while two ducks (for reasons known only to them) are simultaneously trying to empty it.
anywhere in this book). Only the most basic mathematical operations will be used (addition, subtraction, multiplication, and division, plus a couple of more advanced terms such as powers and roots), but that does not mean that you wont be required to engage in some deep thinking. I also did my best to keep the text light and give it an amusing lilt nobody really likes questions about three ducks who are filling a pool while two ducks (for reasons known only to them) are simultaneously trying to empty it.