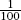PARADOXES IN MATHEMATICS
STANLEY J. FARLOW
DOVER PUBLICATIONS, INC.
Mineola, New York
Copyright
Copyright 2014 by Stanley J. Farlow
All rights reserved.
Bibliographical Note
Paradoxes in Mathematics is a new work, first published by
Dover Publications, Inc., in 2014.
International Standard Book Number
eISBN-13: 978-0-486-79173-9
Manufactured in the United States by Courier Corporation
49716X01 2014
www.doverpublications.com

Dedication Ali Ozluk (19522012)
Twenty years ago my colleague, good friend, and very good number theorist Ali Ozluk came into my office and suggested we write a book together titled something like, Believe It or Not: Paradoxes in Mathematics, which detailed many of the unexpected and surprising results in mathematics. I thought the idea was splendid so I started writing some short pieces describing what I thought were some unusual and startling results in mathematics. But Ali was deeply involved in his research in number theory, working on the distribution of the roots of the Riemann zeta function, in which he made several important contributions, so he put his suggestion on hold. To make a long story short, while Ali was deep in number theory, I wrote an entire book on his suggestion and told Ali that we should publish it together, but being the gracious person he was, he insisted that I publish it on my own.
Unfortunately, Ali died unexpectedly on March 1, 2012 and although he never saw his suggestion come to fruition, it is my great privilege to dedicate this book to my good friend and very good number theorist, Ali Ozluk. We miss you, Ali.
Table of Contents
Introduction
As a goodwill gesture for buying this overpriced book, the author would like to present you with the last piece of his famous blueberry pie, as shown in . Feel free to choose either Pie A or Pie B. You say you prefer Pie A? Certainly, it is the larger piece. Or is it? Before you make your final decision, you may want to turn the page upside down and take another peek. You see, things are not always as they seem; your brain may be deceiving you.
According to Martin Gardner in his book, Riddles of the Sphinx, this optical illusion, which shows Pie A as the larger piece when the book is right-side up, and Pie B as the larger piece when the book is upside down, is due to the science fiction writer Fred Flanagan. According to Mr. Flanagan, it isnt really an illusion at all, it just looks like one.
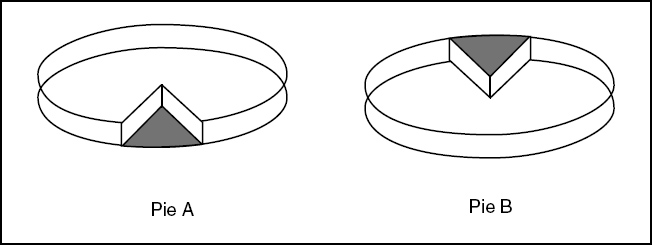
Figure 1
To psychologists, an optical illusion is something we perceive visually in a deceptive and misleading manner, which is another way of saying information taken in by the eye and processed by the brain doesnt quite jibe with the object under observation. The fact of the matter is our brains sometimes add to what our eyes report and sometimes what it adds is not, well, lets say, 100% accurate. But we shouldnt always blame our brains. Sometimes our eyes are the culprit; they sometimes filter out information and leave it to our brains to fill in the gaps, which it sometimes does incorrectly.
The history of civilization is full of obvious truths which later were proven to be obvious falsehoods. No one gave Aristotle a second thought when he said, Heavy falls fast, light falls slow. It took 2,000 years before a man from Pisa, Italy proved him wrong.
This book is about paradoxes in mathematics, which in a way is a paradox in itself. Also, people are not in complete agreement on what is a paradox. For some, a paradox refers to a phenomenon thats baffling and the resolution of the phenomenon is beyond current understanding. The word paradox comes from Greek: para = beyond and doxa = opinion. Other people relax the meaning of the word and argue that a paradox resolved is still a paradox. But others argue that once a paradox is solved it is no longer a paradox; it is simply part of an accepted belief system or theory. Many paradoxes in logic, such as Russells Paradox, which played a major role in the development of logic and axiomatic set theory, are of this type. They may not be considered paradoxes to professional logicians, but they are still conundrums to the general public. (Just ask someone to resolve Russells Barber Paradox.) Other people adopt a more liberal meaning of a paradox to include phenomena whose outcomes are surprising and nonintuitive, but whose solution can be resolved easily with mathematics. These phenomena are more of the believe it or not type of paradoxes. The Rope-Around-the-Earth Paradox in this book is this type. The most liberal interpretation of a paradox is the mathematical illusion, where a mathematical sleight of hand is performed on an unwary observer. The tale of Uncle Georges Will in this book is such an example. Although most people would not consider this to be a paradox, the puzzled look of the observer is still the same. This book includes all these interpretations of a paradox, and it will be the readers duty to determine into which category a given story falls.
The study of paradoxes broadens the mind. Some are of the aha category, where after some thought you say, Why didnt I think of that? There are others, however, such as the Two-Envelope Paradox, which (arguably) has never been completely resolved, although several people have claimed, quite vociferously, to have done so. The really good paradoxes are those which we cant resolve without broadening our understanding of the underlying theory or foundations of the paradox. Many paradoxes are responsible for the clarification of basic concepts and are responsible for the introduction of new ideas. E.T. Bell once said, One of the endlessly alluring aspects of mathematics is that its thorniest paradoxes have a way of blooming into beautiful theories.
Paradoxes in logic, such as the Liars Paradox and Russells Barber Paradox, forced logicians to modify existing theories to rid themselves of troubling inconsistencies. The Liar Paradox, credited to the Greek philosopher Eubulides of Miletus, who lived around 400 B.C., states:
A man says, I am lying.
If this statement is a lie, then in fact he is not lying.
If this statement is not a lie, then in fact he is lying.
In other words, he is lying and he is not lying.
This is an example of the many types of paradoxes you will discover in this book. Enjoy.
Jerry Farlow
Martin Gardner, Riddles of the Sphinx. New Mathematical Library, Vol. 32. 1987.
E. T. Bell. The Development of Mathematics. 2nd Edition. McGraw-Hill, 1945.
Paper Folding: Do Not Try This at Home
For our first paradox, we present the famous Paper Folding Paradox, one that has been presented in various venues for a thousand years, but nevertheless never fails to impress the unwary observer. The interesting thing about this paradox is that even after the solution is presented and proven positively, unequivocally to be 100% true, there are still nonbelievers who just dont find it in their hearts to accept the conclusion. So, heres the problem. Try to guess the answer, or at least a guesstimate in the general ballpark.

Suppose you take a piece of paper, like the one you are looking at right now, and suppose for simplicitys sake it is 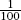
Next page