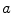Frazer Jarvis - Algebraic Number Theory
Here you can read online Frazer Jarvis - Algebraic Number Theory full text of the book (entire story) in english for free. Download pdf and epub, get meaning, cover and reviews about this ebook. year: 2014, publisher: Springer, genre: Children. Description of the work, (preface) as well as reviews are available. Best literature library LitArk.com created for fans of good reading and offers a wide selection of genres:
Romance novel
Science fiction
Adventure
Detective
Science
History
Home and family
Prose
Art
Politics
Computer
Non-fiction
Religion
Business
Children
Humor
Choose a favorite category and find really read worthwhile books. Enjoy immersion in the world of imagination, feel the emotions of the characters or learn something new for yourself, make an fascinating discovery.
- Book:Algebraic Number Theory
- Author:
- Publisher:Springer
- Genre:
- Year:2014
- Rating:5 / 5
- Favourites:Add to favourites
- Your mark:
Algebraic Number Theory: summary, description and annotation
We offer to read an annotation, description, summary or preface (depends on what the author of the book "Algebraic Number Theory" wrote himself). If you haven't found the necessary information about the book — write in the comments, we will try to find it.
The technical difficulties of algebraic number theory often make this subject appear difficult to beginners. This undergraduate textbook provides a welcome solution to these problems as it provides an approachable and thorough introduction to the topic.
Algebraic Number Theory takes the reader from unique factorisation in the integers through to the modern-day number field sieve. The first few chapters consider the importance of arithmetic in fields larger than the rational numbers. Whilst some results generalise well, the unique factorisation of the integers in these more general number fields often fail. Algebraic number theory aims to overcome this problem. Most examples are taken from quadratic fields, for which calculations are easy to perform.
The middle section considers more general theory and results for number fields, and the book concludes with some topics which are more likely to be suitable for advanced students, namely, the analytic class number formula and the number field sieve. This is the first time that the number field sieve has been considered in a textbook at this level.
Frazer Jarvis: author's other books
Who wrote Algebraic Number Theory? Find out the surname, the name of the author of the book and a list of all author's works by series.
Algebraic Number Theory — read online for free the complete book (whole text) full work
Below is the text of the book, divided by pages. System saving the place of the last page read, allows you to conveniently read the book "Algebraic Number Theory" online for free, without having to search again every time where you left off. Put a bookmark, and you can go to the page where you finished reading at any time.
Font size:
Interval:
Bookmark:
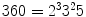is the prime factorisation of 360. However, we should notice that there are already senses in which this factorisation is not really unique; we can write 
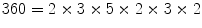, or even 
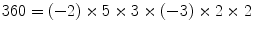. Nevertheless, we can see that all these factorisations are essentially the same, in a way which we could make precise, and we will do so later.
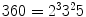is the prime factorisation of 360. However, we should notice that there are already senses in which this factorisation is not really unique; we can write 
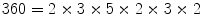, or even 
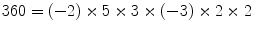. Nevertheless, we can see that all these factorisations are essentially the same, in a way which we could make precise, and we will do so later.
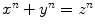has no solutions with 
, 
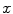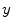and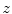 
positive integers when 
.
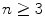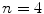, it is easy to see that it suffices to treat the case where 
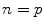, an odd prime. Then we can write the equation in the conjecture as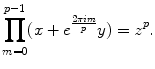 
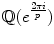. Unfortunately, it turns out that these cyclotomic fields do not, in general, have such a unique factorisation property. This failure of unique factorisation led KummerKummer, Ernst Eduard to develop the theory of idealsIdeal, and factorisation of ideals, which is the starting point for algebraic number theory.
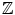can be addressed using arithmetic in a larger set, and where unique factorisation in this set is a crucial requirement.
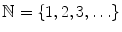. In order to study factorisation in the natural numbers, we need some basic definitions.
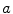and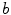 
be integers. Then 
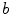divides Divides 
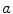, or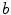 
is a factor Factor or divisor Divisor of 
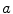, if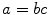 
for some integer 
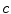. Write 
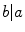to mean that 
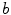divides 
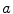and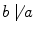 
to mean that 
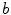does not divide 
.
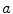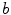divides 
Font size:
Interval:
Bookmark:
Similar books «Algebraic Number Theory»
Look at similar books to Algebraic Number Theory. We have selected literature similar in name and meaning in the hope of providing readers with more options to find new, interesting, not yet read works.
Discussion, reviews of the book Algebraic Number Theory and just readers' own opinions. Leave your comments, write what you think about the work, its meaning or the main characters. Specify what exactly you liked and what you didn't like, and why you think so.