Universitext
Series Editors
Sheldon Axler
San Francisco State University, San Francisco, CA, USA
Carles Casacuberta
Universitat de Barcelona, Barcelona, Spain
John Greenlees
University of Warwick, Coventry, UK
Angus MacIntyre
Queen Mary University of London, London, UK
Kenneth Ribet
University of California, Berkeley, CA, USA
Claude Sabbah
cole Polytechnique, CNRS, Universit Paris-Saclay, Palaiseau, France
Endre Sli
University of Oxford, Oxford, UK
Wojbor A. Woyczyski
Case Western Reserve University, Cleveland, OH, USA
Universitext is a series of textbooks that presents material from a wide variety of mathematical disciplines at master's level and beyond. The books, often well class-tested by their author, may have an informal, personal even experimental approach to their subject matter. Some of the most successful and established books in the series have evolved through several editions, always following the evolution of teaching curricula, into very polished texts. is a series of textbooks that presents material from a wide variety of mathematical disciplines at masters level and beyond. The books, often well class-tested by their author, may have an informal, personal even experimental approach to their subject matter. Some of the most successful and established books in the series have evolved through several editions, always following the evolution of teaching curricula, into very polished texts.
Thus as research topics trickle down into graduate-level teaching, first textbooks written for new, cutting-edge courses may make their way intoThus as research topics trickle down into graduate-level teaching, first textbooks written for new, cutting-edge courses may make their way intoUniversitext..
More information about this series at http://www.springer.com/series/223
Olivier Bordells
Arithmetic Tales
Advanced Edition
2nd ed. 2020
Logo of the publisher
Olivier Bordells
2 alle de la combe, Aiguilhe, France
Translated by Vronique Bordells
ISSN 0172-5939 e-ISSN 2191-6675
Universitext
ISBN 978-3-030-54945-9 e-ISBN 978-3-030-54946-6
https://doi.org/10.1007/978-3-030-54946-6
Mathematics Subject Classication (2010): 11-01 11A 11L07 11M06 11N05 11N13 11N25 11N37 11R04 11R09 11R11 11R16 11R18 11R21 11R27 11R29 11R42
Springer Nature Switzerland AG 2020
This work is subject to copyright. All rights are reserved by the Publisher, whether the whole or part of the material is concerned, specifically the rights of translation, reprinting, reuse of illustrations, recitation, broadcasting, reproduction on microfilms or in any other physical way, and transmission or information storage and retrieval, electronic adaptation, computer software, or by similar or dissimilar methodology now known or hereafter developed.
The use of general descriptive names, registered names, trademarks, service marks, etc. in this publication does not imply, even in the absence of a specific statement, that such names are exempt from the relevant protective laws and regulations and therefore free for general use.
The publisher, the authors and the editors are safe to assume that the advice and information in this book are believed to be true and accurate at the date of publication. Neither the publisher nor the authors or the editors give a warranty, expressed or implied, with respect to the material contained herein or for any errors or omissions that may have been made. The publisher remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
This Springer imprint is published by the registered company Springer Nature Switzerland AG.
The registered company address is: Gewerbestrasse 11, 6330 Cham, Switzerland
Preface
Significant advances have been made in number theory since the book Arithmetic Tales was published back in 2012. The most important breakthrough is probably the landmark result that Zhang proved on the bounded gaps between prime numbers. One of the main achievements of the proof is to establish a suitable extension of the BombieriVinogradov theorem.
This naturally led me to write a thoroughly revised and updated version of the book. To begin with, the chapters devoted to the knowledge required from undergraduate mathematics students have all been removed. In particular, this includes practically all of the content of my earlier book Thmes dArithmtiques, with only the most necessary overlapping content completely rewritten in summarized form. The prerequisites for this second edition are therefore essentially all known results in classic elementary number theory. Besides, the sections previously called Further Developments have become full sections that have substantially been expanded. In addition, the number of exercises, all corrected as in the first edition, has increased by almost 50%.
Each chapter has been revised, updated and enhanced, and Chap. in particular has undergone some drastic alterations. Dirichlet series are now to be found at the beginning of the chapter immediately after the basic theory. A quite simple asymptotic formula has been derived for multiplicative functions close to the divisor functions. Each mean value of the usual arithmetic function is given in detail, including the important Hooleys divisor function. A section, that is rarely mentioned in the literature and dealing with arithmetic functions of several variables, is provided. Ten well-known problems in analytic number theory have also been selected and given with almost self-contained proofs. The results that are beyond the scope of this book are given without proof but always with one or several references, so that the reader who is eager to learn more about the subject may go deeper into the analysis and pursue further so as to absorb the most profound results of the subject area.
This revised edition would have been impossible without the patience, availability and enthusiasm of Remi Lodh, whom I wish to thank for his interest in this project. I would also like to thank most warmly my wife, Vronique, for her rigorous and faithful translation of this work and for her unrelenting support. I am also most grateful to my colleagues Anne-Lise Camus, Florian Daval and Igor E. Shparlinski for their careful proof-reading and to Wadysaw Narkiewicz and Titus W. Hilberdink for their suggestions. Last but not least, I would particularly like to thank my two children, Nicolas, a graduate student in Civil and Mining Engineering at the Ecole des Mines, and Marie, who follows a 2-year undergraduate intensive course in Mathematics, Physics and Biology.
Olivier Bordells
Aiguilhe, France
May 2020
Preliminaries
General Notation
Letters n, m and a, b, c, d, k, refer to integers, whereas p indicates a prime number. We also adopt Riemanns notation for complex numbers, namely 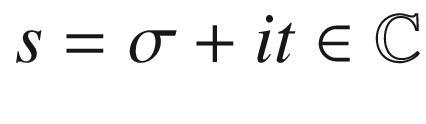 with
with 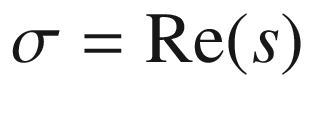















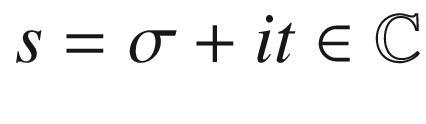 with
with