ADVANCED
TRIGONOMETRY ADVANCED
TRIGONOMETRY C.V. DURELL
AND A. ROBSON DOVER PUBLICATIONS, INC.
MINEOLA, NEW YORK Bibliographical Note This Dover edition, first published in 2003, is an unabridged republication of the work originally published by G. Bell and Sons, Ltd., London, in 1930. Library of Congress Cataloging-in-Publication Data Durell, Clement V (Clement Vavasor), b. 1882.
Advanced trigonometry / C.V. Durell and A. Robson. p. cm. Originally published: London : G.
Bell and Sons, Ltd., 1930. Includes index. ISBN 0-486-43229-7 (pbk.) 1. Trigonometry. I. (Alan), b. 1888. II. Title. Title.
QA531.D786 2003 516.24dc21 2003057276 Manufactured in the United States of America
Dover Publications, Inc., 31 East 2nd Street, Mineola, N.Y. 11501 PREFACE MOST teachers will agree that at the present time the work of mathematical specialists in schools is heavily handicapped by the absence of suitable text-books. There have been such radical changes in method and outlook that it has become necessary to treat large sections of some of the standard books merely as (moderately) convenient collections of examples and to supply the bookwork in the form of notes ; especially is this true of Algebra, Trigonometry, and the Calculus. Dividing lines between these subjects tend nowadays to be obliterated. Methods of the Calculus are freely used in courses of Algebra and Trigonometry, while matter which used to find a place in the Algebra text-book is now included more conveniently elsewhere. Perhaps the most important example of this re-arrangement is the treatment of the logarithmic function.
For many years past leading mathematicians have advocated a definition which transfers the chapter on the theory of logarithms from the Algebra to the Calculus text-book, and makes it the basis from which the exponential function is discussed, thus reversing the order commonly followed. The authors are convinced by their own experience that this is the best mode of approach. On general principles it would seem desirable also to follow the same order for the Complex variable, but unfortunately in practice this point of view appears to be too difficult for school work. By tradition the theory of the exponential and logarithmic functions of a complex variable is included in books on Advanced Trigonometry and this is a very reasonable arrangement ; it seems equally desirable to include also the theory of the corresponding functions of a real variable instead of relegating it to the Calculus book. The interest and value of advanced trigonometry lies in regarding it as an introduction to modern analysis. The methods by which results are obtained are often more importantthat is, educationally more valuablethan the results themselves.
The character of the treatment in this book is shaped and controlled by that idea. Thus the methods for expanding functions in series focus attention on remainders and limits ; the methods for factorizing functions turn on establishing possible forms and then using the fundamental factor-theorem ; the discussion of complex numbers emphasises the fact that complex numbers are just as real as real numbers, etc. For the same reason no apology need be offered for the prevalence, in this book, of inequalities. Their importance in higher mathematics can hardly be exaggerated, and they are invaluable too in elementary work. The useful inequalities of will, it is believed, be found fully worthy of their name. The authors are planning text-books parallel to the present volume on Advanced Algebra and Calculus, written from a similar point of view.
In all these subjects, it must be admitted, there are certain difficulties which the average student will never face, but which are all-important for the real mathematician; these include, for example, the purely arithmetical treatment of real number, limits, continuity, convergence, mean-value theorems, the analysis of area, length of a curve, etc. The authors propose to deal with these matters in a book which is cited as a companion volume on Analysis, limiting the treatment, however, to what seems suitable for specialist work at schools. Although planned, no part of this book is yet written. The theory of Infinite Products has been left for this companion volume ; it is not so easy to provide a satisfactory ab initio treatment for products as it is for series and the alternative of taking for granted everything that really matters is undesirable. Happily also Infinite Products are of small value in elementary work and they are not required for most examinations. however, pp. 223, 240. 223, 240.
As a text-book on Trigonometry, this volume is a continuation of Durell and Wrights Elementary Trigonometry, and , which deals with a difficult subject and one which should be done carefully if it is done at all. A Key is published, for the convenience of teachers, in which solutions are given in considerable detail, and in some cases alternative methods of solution are supplied, so that to some extent the Key forms a supplementary teaching manual. The authors gratefully acknowledge help with the proofs received from Mr. J. C. CHAPTER IPROPERTIES OF THE TRIANGLE A LIST of the fundamental formulae connecting the elements of a triangle, proofs of which have been given in Durell and Wrights Elementary Trigonometry, will be found in Section D of the formulae at the beginning of that book ; references to these proofs will be indicated by the prefix E.T. For geometrical proofs of theorems on the triangle, the reader is referred to some geometrical text-book. CHAPTER IPROPERTIES OF THE TRIANGLE A LIST of the fundamental formulae connecting the elements of a triangle, proofs of which have been given in Durell and Wrights Elementary Trigonometry, will be found in Section D of the formulae at the beginning of that book ; references to these proofs will be indicated by the prefix E.T. For geometrical proofs of theorems on the triangle, the reader is referred to some geometrical text-book.
When these theorems are quoted or illustrated in this chapter, references, indicated by the prefix M.G., are given to Durells Modern Geometry. Revision. Examples for the revision of ordinary methods of solving a triangle are given in , below. It is sometimes convenient to modify the process of solution. If, for example, the numerical values of b, c, A are given and if the value of a only is required, we may proceed as follows : 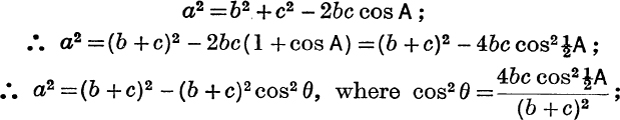
 where
where 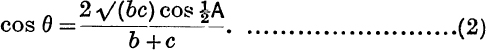 is first found from (), both equations being adapted to logarithmic work. An angle , used in this way, is called a subsidiary angle. 21 to 25. EXERCISE I. a. [Solution of Triangles] 1. a. [Solution of Triangles] 1.
is first found from (), both equations being adapted to logarithmic work. An angle , used in this way, is called a subsidiary angle. 21 to 25. EXERCISE I. a. [Solution of Triangles] 1. a. [Solution of Triangles] 1.
What are the comparative merits of the formulae for cos A, cos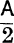 , sin
, sin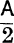 , tan
, tan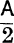 , when finding the angles of a triangle from given numerical values of a, b, c ? . Given a = 100, b = 80, c = 50, find A. Given a
, when finding the angles of a triangle from given numerical values of a, b, c ? . Given a = 100, b = 80, c = 50, find A. Given a
Next page







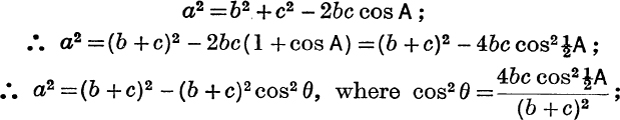
 where
where 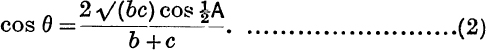 is first found from (), both equations being adapted to logarithmic work. An angle , used in this way, is called a subsidiary angle. 21 to 25. EXERCISE I. a. [Solution of Triangles] 1. a. [Solution of Triangles] 1.
is first found from (), both equations being adapted to logarithmic work. An angle , used in this way, is called a subsidiary angle. 21 to 25. EXERCISE I. a. [Solution of Triangles] 1. a. [Solution of Triangles] 1.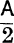 , sin
, sin