Lopez C.P. - Differential Calculus using Mathematica
Here you can read online Lopez C.P. - Differential Calculus using Mathematica full text of the book (entire story) in english for free. Download pdf and epub, get meaning, cover and reviews about this ebook. genre: Science. Description of the work, (preface) as well as reviews are available. Best literature library LitArk.com created for fans of good reading and offers a wide selection of genres:
Romance novel
Science fiction
Adventure
Detective
Science
History
Home and family
Prose
Art
Politics
Computer
Non-fiction
Religion
Business
Children
Humor
Choose a favorite category and find really read worthwhile books. Enjoy immersion in the world of imagination, feel the emotions of the characters or learn something new for yourself, make an fascinating discovery.
Differential Calculus using Mathematica: summary, description and annotation
We offer to read an annotation, description, summary or preface (depends on what the author of the book "Differential Calculus using Mathematica" wrote himself). If you haven't found the necessary information about the book — write in the comments, we will try to find it.
Limits Of Sequences
Limits Of Functions. Lateral Limits
Continuity
Several Variables: Limits And Continuity. Characterization Theorems
Iterated And Directional Limits
Continuity In Several Variables
Numerical Series And Power Series
Series. Convergence Criteria
Numerical Series With Non-Negative Terms
Alternating Numerical Series
Power Series
Power Series Expansions And Functions
Taylor And Laurent Expansions
Derivatives And Applications. One And Several Variables
The Concept Of The Derivative
Calculating Derivatives
Tangents, Asymptotes, Concavity, Convexity, Maxima And Minima, Inflection Points And Growth
Applications To Practical Problems
Partial Derivatives
Implicit Differentiation
Derivability In Several Variables
Differentiation Of Functions Of Several Variables
Maxima And Minima Of Functions Of Several Variables
Conditional Minima And Maxima. The Method Of Lagrange Multipliers
Some Applications Of Maxima And Minima In Several Variables
Vector Differential Calculus And Theorems In Several Variables
Concepts Of Vector Differential Calculus
The Chain Rule
The Implicit Function Theorem
The Inverse Function Theorem
The Change Of Variables Theorem
Taylors Theorem With N Variables
Vector Fields. Curl, Divergence And The Laplacian
Coordinate Transformation
Differential Equations
Separation Of Variables
Homogeneous Differential Equations
Exact Differential Equations
Linear Differential Equations
Numerical Solutions To Differential Equations Of The First Order
Ordinary High-Order Equations
Higher-Order Linear Homogeneous Equations With Constant Coefficients
Non-Homogeneous Equations With Constant Coefficients. Variation Of Parameters
Non-Homogeneous Linear Equations With Variable Coefficients. Cauchy-Euler Equations
The Laplace Transform
Systems Of Linear Homogeneous Equations With Constant Coefficients
Systems Of Linear Non-Homogeneous Equations With Constant Coefficients
Higher Order Equations And Approximation Methods
The Euler Method
The RungeKutta Method
Differential Equations Systems By Approximate Methods
Differential Equations In Partial Derivatives
Orthogonal Polynomials
Lopez C.P.: author's other books
Who wrote Differential Calculus using Mathematica? Find out the surname, the name of the author of the book and a list of all author's works by series.
Differential Calculus using Mathematica — read online for free the complete book (whole text) full work
Below is the text of the book, divided by pages. System saving the place of the last page read, allows you to conveniently read the book "Differential Calculus using Mathematica" online for free, without having to search again every time where you left off. Put a bookmark, and you can go to the page where you finished reading at any time.
Font size:
Interval:
Bookmark:
Differential Calculus usingMATHEMATICACSAR PREZ LPEZ
INDEX
Chapter 1. Limits AND CONTINUITY. ONE and several VARIABLES Mathematica provides commands that allow you tocalculate virtually all types of limits. The same functions are used tocalculate limits of sequences and limits of functions. The commands for theanalysis of one and several variables are similar. In this chapter we willpresent numerous exercises which illustrate Mathematicas capabilities in thisfield.
The syntax of the commands concerning limits are presented below: Limit(sequence, n->infinity) calculates the limit as n tends to infinity of the sequencedefined by its general term.Nlimit(sequence, n->infinity)calculates the limit as n tends to infinity of the sequence definedby its general term. This function is implemented in the package"Numerical Math" and is used when the Limit function can not solvethe problemLimit(function,x->a) calculates the limit of the function of the variablex, indicated by its analytical expression, as the variable xtends towards the value a.Nlimit(function, x->a) calculatesthe limit of the function of the variable x, indicated by its analyticalexpression, as the variable x tends towards the value a. Thisfunction is implemented in the package "Numerical Math" and is usedwhen the Limit function can not solve the problemLimit(function, x->a,Direction->1)calculates the limit of thefunction of the variable x, indicated by its analytical expression, as thevariable x tends to the value a from the right .Limit(function,x->a, Direction->1)calculates the limit of thefunction of the variable x, indicated by its analytical expression, as thevariable x tends to the value a from the left .
, 
, 
, 
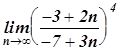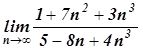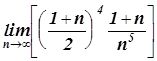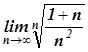In the first two limits we face the typical uncertaintygiven by the quotient 
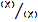: In[1]:=Limit[((2n-3)/(3n-7))^4, n->Infinity]16/81In[2]:= Limit[(3n^3+7 n^2+1)/(4 n^3-8 n+5), n->Infinity] - The last two limits present an uncertainty of the form 
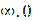and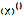 
: In[1]:=Limit[((n+1)/2)((n^4+1)/n^5), n->Infinity]-In[2]:=Limit[((n+1)/n^2)^(1/n), n->Infinity]Exercise 1-2. Calculatethe following limits:
, 
, 
, 
, 
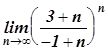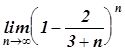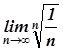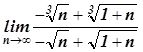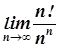The first two examples are indeterminate of the form 
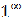: In[1]:=Limit[((n+3)/(n-1))^n,n->Infinity]EIn[2]:=Limit[(1-2/(n+3))^n,n->Infinity]-2E The next two limits are of the form and 
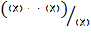: In[1]:=Limit[(1/n)^(1/n),n->Infinity]In[2]:=Limit[((n+1)^(1/3)-n^(1/3))/((n+1)^(1/2)-n^(1/2)), n->Infinity] The last limit is of the form : In[2]:=Limit[n!/n^n,n->Infinity]Series::esss:Essential singularityencountered in1 3Gamma[- + 1 + O[n] ].nSeries::esss:Essential singularity encountered in1 3Gamma[- + 1 + O[n] ].nn!Limit[--, n -> Infinity]nn The Limit function does not solve the problem. We use Nlimit, andload the appropriate package, if it is not already in memory. In[3]:=<In[4]:=NLimit[n!/n^n,n->Infinity]
Some exercises are accompanied by graphics. The useof graphics is advisable if there are any doubts concerning the results. Exercise 1-3. Calculatethe following limits:
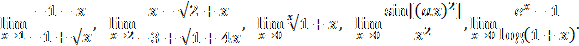Initially, we have fourindeterminates of type 
and one of the form : In[1]:=Limit[(x-1)/(x^(1/2)-1),x->1]In[2]:=Limit[(x-(x+2)^(1/2))/((4x+1)^(1/2)-3),x->2]-In[1]:= Limit[(1+x)^(1/x),x->0]EIn[3]:=Limit[Sin[ax]^2/x^2,x->0]aExercise 1-4. Calculatethe following function limits:
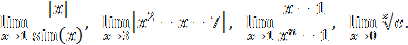The first limit is calculated as follows: In[1]:=Limit[Abs[x]/Sin[x],x->0]Limit[Abs[x] Csc[x],x -> 0]In[2]:=Limit[Abs[x]/Sin[x],x->0,Direction->1]Limit[Abs[x] Csc[x],x -> 0, Direction -> 1]In[3]:=Limit[Abs[x]/Sin[x],x->0,Direction->-1]Limit[Abs[x] Csc[x],x -> 0, Direction -> -1] We note that we can not calculate directly, or thelimit of the function, or the lateral limits. In[1]:=Limit[x/Sin[x],x->0]In[2]:=Limit[-x/Sin[x],x->0]-1 Then the function has no limit if x->0. In[1]:=Limit[x/Sin[x],x->0]In[2]:=Limit[-x/Sin[x],x->0]-1 Then the function has no limit if x->0.
For the next two limits we have: In[1]:=Limit[Abs[x^2-x-7],x->3]Limit[Abs[-7 - x + x ], x ->3] Directly, Mathematica does not offer the result ofthis limit, but we know that the limit of a function module is the limit modulefunction. In[2]:=Abs[Limit[x^2-x-7,x->3]] Another way to solve this problem is to use the Nlimit
Font size:
Interval:
Bookmark:
Similar books «Differential Calculus using Mathematica»
Look at similar books to Differential Calculus using Mathematica. We have selected literature similar in name and meaning in the hope of providing readers with more options to find new, interesting, not yet read works.
Discussion, reviews of the book Differential Calculus using Mathematica and just readers' own opinions. Leave your comments, write what you think about the work, its meaning or the main characters. Specify what exactly you liked and what you didn't like, and why you think so.