Numerical Methods:Nonlinear Equations,Numerical Calculus,& Differential Equationsby D. James Benton Copyright 2018-2021 by D. James Benton, all rights reserved.
Preface
This is a combination of three books:
Nonlinear Equations ,
Numerical Calculus , and
Differential Equations . These three topics combine to form
Numerical Methods . Nonlinear, integral, and differential equations are found throughout science and engineering across a wide variety of disciplines.
These are a significant part of applied mathematics and much effort has been devoted to their study and solution. We will consider single and multi-variable problems. Various theories will be presented, but always with a focus on what works bestthat is, robust algorithms.
The Finite Element Method
If you've struggled to understand the finite element method, then you must read this book. I don't cover a lot of theory in this text. It's mostly a compilation of examples.
The one theoretical aspect of numerical methods for solving differential equations that I will present is the finite element method. This powerful technique is more often than not buried under a mountain of esoteric details that make it inaccessible to most students of applied mathematics. I aim to reveal, not obfuscate. I trust you will find this book helpful in that respect.
Programming
Most of the examples in this book are implemented in the C programming language. Some are contained in Excel spreadsheets with macros.
All of the program source codes (including a triangular grid generator and vectorized matrix solvers) are included. All of the programs will run on any version of Windows. All of the examples contained in this book, (as well as a lot of free programs) are available at: http://www.dudleybenton.altervista.org/software/index.html All of the color figures can be found here (click on cover): http://djamesbenton.altervista.org/ 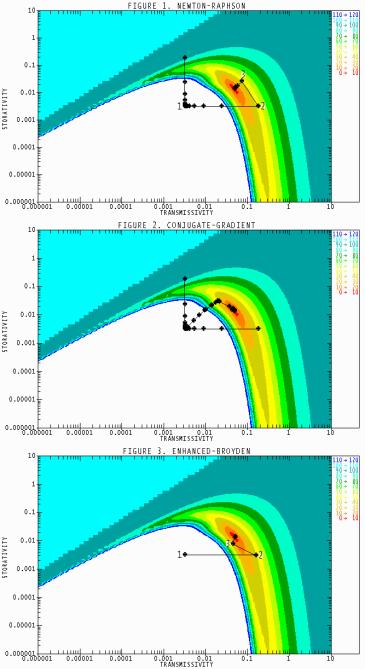
| Table of Contents | page |
| Preface | i |
| Chapter 1. Single-Valued Functions of One Variable | |
| Chapter 2. Multi-Valued Functions of One Variable | |
| Chapter 3. Functions of Several Variables | |
| Chapter 4: Bounding & Scaling | |
| Chapter 5: Nonlinear Least-Squares | |
| Chapter 6: Quasi-Newton Methods | |
| Chapter 7. Broyden's Derivative-Free Algorithm | |
| Chapter 8. Approximating Gradients and Hessians | |
| Chapter 9. Multi-Dimensional Bisection Search | |
| Chapter 10: Evolutionary Method | |
| Chapter 11: Nonlinear Regression | |
| Chapter 12: Hybrid Regression | |
| Chapter 13. Data Analysis | |
| Chapter 14. Newton-Cotes Integration | |
| Chapter 15. Gauss Quadrature | |
| Chapter 16. Chebyshev & Lobatto Quadrature | |
| Chapter 17. Composite Rules | |
| Chapter 18. Green's Lemma | |
| Chapter 19. 2D and 3D Integrals | |
| Chapter 20. Improper Integrals | |
| Chapter 21 Applications | |
| Chapter 22. Differential Equations | |
| Chapter 23. Explicit Runge-Kutta Methods | |
| Chapter 24. Marching Method Applications | |
| Chapter 25. Step Length Control | |
| Chapter 26. Finite Difference Method | |
| Chapter 27. Finite Element Method | |
| Chapter 28. Boundary Element Method | |
| Appendix A: Steam Properties - A Practical Example | |
| Appendix B: Graphical Representation | |
| Appendix C: Data Transformation Program | |
| Appendix D. Newton-Cotes Coefficient Program | |
| Appendix E. Gauss Quadrature Weights & Abscissas | |
| Appendix F. Cooling Tower Demand | |
| Appendix G: Generalized Runge-Kutta Function | |
| Appendix H: Finite Difference Operators | |
| Appendix I: Processing and Checking Finite Element Models | |
| Appendix J: Solving Large Systems of Linear Equations | |
| Appendix K: Triangular Element Generating Program | |
| Appendix L: SIAM Paper | |


Chapter 1. Single-Valued Functions of One Variable
The simplest problem we can consider is that of single-valued, real functions of one variablethat is,
y(x) where
y has one-and-only-one value for each
x and there is only one value of
x for any value of
y . This excludes functions that wrap around, fold back on themselves, oscillate, or take on complex values, such as sin(x), cos(x), and 1-x. One such function is illustrated in the following figure:
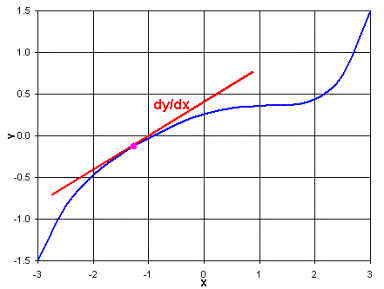
Most discussions presume you're interested in
y(x)=0 .
For some other target value, simply subtract y'(x)=y(x)-target and solve the modified problem. We will consider several methods for solving this problem.
Newton-Raphson Method
The Newton-Raphson Method begins with a guess (e.g., the purple dot in the preceding figure), the value of the function at that position, and the slope (or first derivative) of the function at that point. [1] The next guess (or
provisional value ) is calculated from the current one by taking the difference between the target and current value of the function and dividing this by the slope.
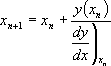
(1.1) This method works well some of the time, but not always. It may converge rapidly or not at all.
If the root (i.e., where y=0 ) lies in a region of x where dy/dx is small, changes sign, or vanishes (e.g., near x=1.33 in the preceding figure), you've got a real problem, because the iteration implied by Equation 1.1 will diverge (i.e., blow up ). This is why you never want to use the raw, unqualified Newton-Raphson Method to solve any routine problemyou can't depend on it always arriving at a valid answer. The illustration we will use for this is solving the properties of steam (or a refrigerant) for unknown density, which you may need to do many, many times in a spreadsheet or other model. Here's what the iterations look like in Excel (sorry about the ratty graphics, but it's the best you can get out of Microsoft). 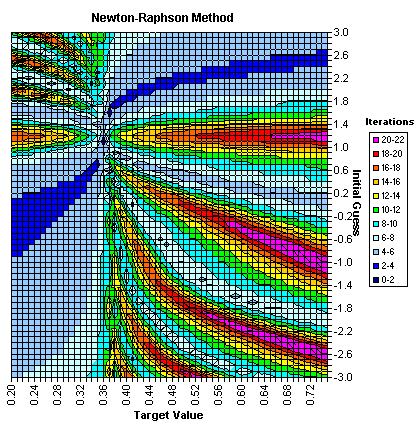 The Newton-Raphson Method always finds a solution with 61x56=3416 cases. The average number of iterations for this example is 9.4.
The Newton-Raphson Method always finds a solution with 61x56=3416 cases. The average number of iterations for this example is 9.4.
The dark blue curving region (corresponding to zero iterations) is the shape of the curve, y(x), when the initial guess is equal (or very close to) the final solution. The red and magenta regions are where it takes 20-22 iterations to arrive at a solution to the specified tolerance (0.000001). If you're lucky and your first guess is close to the final solution (i.e., in the blue areas) this method is quite efficient. If you're not so lucky (i.e., in the yellow, orange, red, or magenta areas), this method isn't efficient. At least it always converges for this examplesomething that is not always true. The Newton-Raphson Method in VBA is: Function NewtonRaphson(target As Double, guess As Double, convergence As Double) As Integer Dim x As Double x = guess NewtonRaphson = 1 'counting function calls While True If (Abs(Y(x) - target) <= convergence) Then Exit Function NewtonRaphson = NewtonRaphson + 1 x = x + (target - Y(x)) / dYdX(x) Wend End Function
Next page












 Most discussions presume you're interested in y(x)=0 .
Most discussions presume you're interested in y(x)=0 . 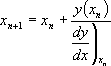 (1.1) This method works well some of the time, but not always. It may converge rapidly or not at all.
(1.1) This method works well some of the time, but not always. It may converge rapidly or not at all.  The Newton-Raphson Method always finds a solution with 61x56=3416 cases. The average number of iterations for this example is 9.4.
The Newton-Raphson Method always finds a solution with 61x56=3416 cases. The average number of iterations for this example is 9.4.