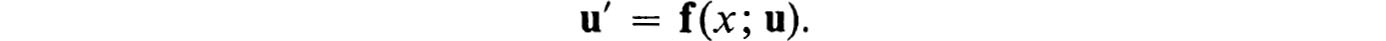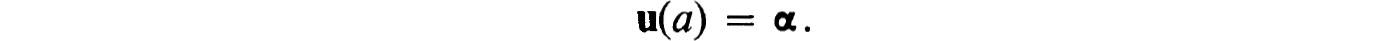Herbert Bishop Keller - Numerical Methods for Two-Point Boundary-Value Problems

To the memory of my parents

Copyright

Copyright 1968 by the Blaisdell Publishing Company

Copyright 1992 by Herbert B. Keller

All rights reserved.

Bibliographical Note

This Dover edition, first published in 2018, is an unabridged, corrected, and expanded republication of the work originally published by the Blaisdell Publishing Company, Waltham, Massachusetts, in 1968. Two appendices have been added following the Index to the original work containing additional material by Herbert B. Keller and 3 co-authors. Bibliographical information concerning these appendices can be found in the Preface to the Dover Edition, and in the acknowledgments at the start of each section. The publisher is grateful to the organizations and journals which gave permission for their material to be reprinted here.

Library of Congress Cataloging-in-Publication Data

Names: Keller, Herbert Bishop, author.

Title: Numerical methods for two-point boundary-value problems / Herbert B. Keller.

Description: Dover edition [2018 edition]. | Mineola, New York : Dover Publications, Inc., 2018. | Originally published: Waltham, Massachusetts : Blaisdell Publishing Company, 1968. Republished by Dover Publications, 1992. 2018 republication includes two new appendices of additional material by author. | Includes bibliographical references and index.

Identifiers: LCCN 2018019764 | ISBN 9780486828343 | ISBN 0486828344

Subjects: LCSH: Boundary value problemsNumerical solutions.

Classification: LCC QA379 .K43 2018 | DDC 515/.35dc23

LC record available at https://lccn.loc.gov/2018019764

Manufactured in the United States by LSC Communications

82834401 2018

www.doverpublications.com

This edition contains numerous minor corrections to the original edition, a new , Some Further Results, containing nine research papers. Of course much recent work, and in particular the development of powerful general purpose codes, could not be included.

Several areas which have been particularly active in the past ten years or so are not well covered. This includes the treatment of boundary layers, adaptive grid generation, collocation methods, path following and bifurcation theory, multiple or parallel shooting and problems posed on infinite intervals. The powerful continuation and bifurcation code AUTO developed by E. Doedel applies and extends the methods of 5.6 (or Appendix C.7) using collocation for solving very general boundary-value problems depending upon parameters. The methods in AUTO include automatic mesh generation and refinement to obtain specified accuracy and to resolve boundary layers. Thus it is a very advanced code and I judge it to be the most powerful such software currently available.

With the rapid development of parallel or concurrent computers we are beginning to see corresponding changes in algorithm development for two-point boundary-value problems. Our choice of the name parallel shooting in 2.4 was based on the early stages of such designs and indeed these methods are becoming more important. The recent interest in dynamical systems is also beginning to influence the numerical methods. In particular the study of homoclinic and heteroclinic orbits must employ methods valid for infinite intervals.

I hope that this somewhat updated edition will help those interested in the theory and practice of solving two-point boundary-value problems.

H. B. K ELLER

Pasadena, May, 1991.

In this monograph we present a brief, elementary yet rigorous account of practical numerical methods for solving very general two-point boundary-value problems. Three techniques are studied in detail: initial value or shooting methods in .

Initial-value methods are seldom advocated in the literature, but we find them extremely practical and theoretically powerful. A modification, called parallel shooting, is introduced to treat those unstable cases (with rapidly growing solutions) for which ordinary shooting may be inadequate. High-order accurate methods are stressed, and the well-developed theory of numerical methods for initial-value problems is employed to obtain corresponding results for boundary-value problems. Continuity techniques (related to imbedding) are discussed and illustrated in the examples.

To help maintain an elementary level, we include in brief ac-counts of some of the basic prerequisites : existence theorems for initial-value and two-point boundary-value problems, numerical methods for initial-value problems and iterative methods for solving nonlinear systems. In addition, several other areas of numerical analysis enter our study, such as numerical quadrature, eigenvalue-eigenvector calculation, and solution of linear algebraic systems. Since so many diverse numerical procedures play an important role, the subject matter of this monograph is useful in motivating, introducing, and/or reviewing more general studies in numerical analysis. The level of presentation is such that the text could be used by well-prepared undergraduate mathematics students. Advanced calculus, basic numerical analysis, some ordinary differential equations, and a smattering of linear algebra are assumed.

Many of the problems contain extensions of the text material and so should at least be read, if not worked out. More difficult problems are starred.

It is a pleasure to acknowledge the helpful advice received from Professor Eugene Isaacson and Mr. Richard Swenson, both of whom read the entire manuscript. The computations for the examples were accomplished by the superior work of W. H. Mitchell at Caltech and J. Steadman at the Courant Institute, N.Y.U. The typing was done by Miss Connie Engle in her usual flawless manner.

Finally, the support of the U.S. Army Research Office (Durham) and the U.S. Atomic Energy Commission is gratefully acknowledged.

H. B. K.

The theory of boundary-value problems for ordinary differential equations relies rather heavily on initial-value problems. Even more significant for the subject of this monograph is the fact that some of the most generally applicable numerical methods for solving boundary-value problems employ initial-value problems. Thus we must assume that the reader is somewhat familiar with the existence and uniqueness theory of, as well as numerical methods for solving, initial-value problems. We shall review here and in some of the basic results required.

Since every nth-order ordinary differential equation can be replaced by an equivalent system of n first-order equations, we confine our attention to first-order systems of the form

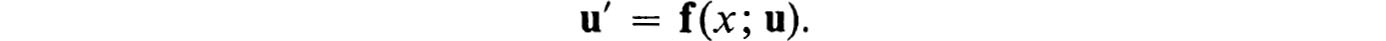
Here u (ul, u2,, un)T is an n-dimensional column vector with the dependent variables uk(x) as components; we say that u(x) is a vector-valued function; f(x;u) is vector-valued with components fk(x, u1,u2,,un), which are functions of the n + 1 variables (x;u). An initial-value problem for the above system is obtained by prescribing at some point, say x = a, the value of u, say