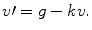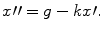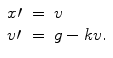Karline Soetaert - Solving Differential Equations in R
Here you can read online Karline Soetaert - Solving Differential Equations in R full text of the book (entire story) in english for free. Download pdf and epub, get meaning, cover and reviews about this ebook. year: 2012, publisher: Springer Science & Business Media, genre: Children. Description of the work, (preface) as well as reviews are available. Best literature library LitArk.com created for fans of good reading and offers a wide selection of genres:
Romance novel
Science fiction
Adventure
Detective
Science
History
Home and family
Prose
Art
Politics
Computer
Non-fiction
Religion
Business
Children
Humor
Choose a favorite category and find really read worthwhile books. Enjoy immersion in the world of imagination, feel the emotions of the characters or learn something new for yourself, make an fascinating discovery.
- Book:Solving Differential Equations in R
- Author:
- Publisher:Springer Science & Business Media
- Genre:
- Year:2012
- Rating:4 / 5
- Favourites:Add to favourites
- Your mark:
Solving Differential Equations in R: summary, description and annotation
We offer to read an annotation, description, summary or preface (depends on what the author of the book "Solving Differential Equations in R" wrote himself). If you haven't found the necessary information about the book — write in the comments, we will try to find it.
Karline Soetaert: author's other books
Who wrote Solving Differential Equations in R? Find out the surname, the name of the author of the book and a list of all author's works by series.











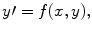
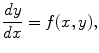
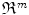 is a vector. Here x is called the independent variable and y = y ( x ) is the dependent variable.
is a vector. Here x is called the independent variable and y = y ( x ) is the dependent variable.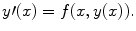
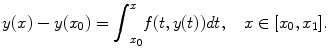
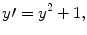
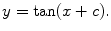
 and we suppose that the function f satisfies some regularity conditions. This is important and we will return to it later.
and we suppose that the function f satisfies some regularity conditions. This is important and we will return to it later.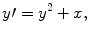


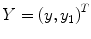 , () we need to specify two conditions to define the solution uniquely in this second order case.
, () we need to specify two conditions to define the solution uniquely in this second order case. , while the air exerts a resistive force which is proportional to the velocity ( v ). The differential equation describing this is:
, while the air exerts a resistive force which is proportional to the velocity ( v ). The differential equation describing this is: