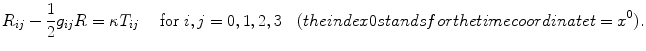Jrgen Jost Graduate Texts in Mathematics Partial Differential Equations 3rd ed. 2013 10.1007/978-1-4614-4809-9_1
Springer Science+Business Media New York 2013
1. Introduction: What Are Partial Differential Equations?
Jrgen Jost 1
(1)
Max Planck Institute for Mathematics in the Sciences, Leipzig, Germany
Abstract
As a first answer to the question, What are PDEs, we would like to give a definition:
As a first answer to the question, What are PDEs, we would like to give a definition:
Definition 1.
A PDE is an equation involving derivatives of an unknown function
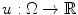
, where is an open subset of
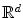
, d 2 (or, more generally, of a differentiable manifold of dimension d 2).
Often, one also considers systems of PDEs for vector-valued functions

, or for mappings with values in a differentiable manifold.
The preceding definition, however, is misleading, since in the theory of PDEs one does not study arbitrary equations but concentrates instead on those equations that naturally occur in various applications (physics and other sciences, engineering, economics) or in other mathematical contexts.
Thus, as a second answer to the question posed in the title, we would like to describe some typical examples of PDEs. We shall need a little bit of notation: A partial derivative will be denoted by a subscript,
In case d =2, we write x , y in place of
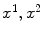
. Otherwise, x is the vector
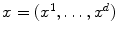
.
Examples.
(1)
The Laplace equation
or, more generally, the Poisson equation
For example, the real and imaginary parts u and v of a holomorphic function
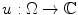
(
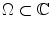
open) satisfy the Laplace equation. This easily follows from the CauchyRiemann equations:
implies
The CauchyRiemann equations themselves represent a system of PDEs. The Laplace equation also models many equilibrium states in physics, and the Poisson equation is important in electrostatics.
(2)
The heat equation: Here, one coordinate t is distinguished as the time coordinate, while the remaining coordinates
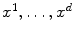
represent spatial variables. We consider
and pose the equation
The heat equation models heat and other diffusion processes.
(3)
The wave equation: With the same notation as in (2), here we have the equation
It models wave and oscillation phenomena.
(4)
The Kortewegde Vries equation
(notation as in (2), but with only one spatial coordinate x ) models the propagation of waves in shallow waters.
(5)
The MongeAmpre equation
or in higher dimensions
with a given function f , is used for finding surfaces (or hypersurfaces) with prescribed curvature.
(6)
The minimal surface equation
describes an important class of surfaces in
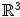
.
(7)
The Maxwell equations for the electric field strength
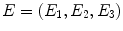
and the magnetic field strength
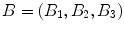
as functions of
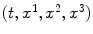
:
where div and curl are the standard differential operators from vector analysis with respect to the variables
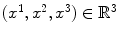
.
(8)
The NavierStokes equations for the velocity v ( x , t ) and the pressure p ( x , t ) of an incompressible fluid of density
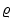
and viscosity :
( d =3,
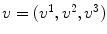
).
(9)
The Einstein field equations of the theory of general relativity for the curvature of the metric ( g ij ) of space-time:
Here, is a constant, T ij is the energymomentum tensor (considered as given), while














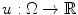 , where is an open subset of
, where is an open subset of 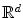 , d 2 (or, more generally, of a differentiable manifold of dimension d 2).
, d 2 (or, more generally, of a differentiable manifold of dimension d 2). , or for mappings with values in a differentiable manifold.
, or for mappings with values in a differentiable manifold.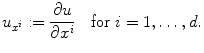
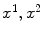 . Otherwise, x is the vector
. Otherwise, x is the vector 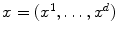 .
.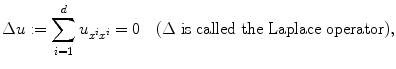
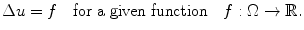
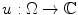 (
( 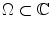 open) satisfy the Laplace equation. This easily follows from the CauchyRiemann equations:
open) satisfy the Laplace equation. This easily follows from the CauchyRiemann equations: 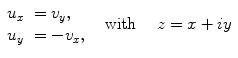
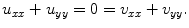
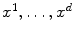 represent spatial variables. We consider
represent spatial variables. We consider 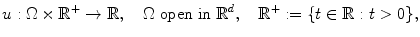
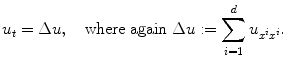
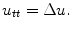
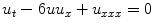
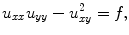
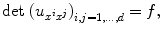
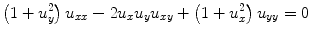
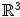 .
.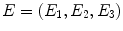 and the magnetic field strength
and the magnetic field strength 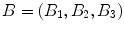 as functions of
as functions of 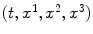 :
: 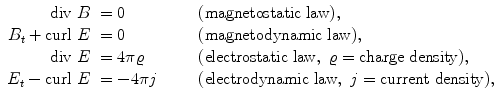
 .
.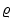 and viscosity :
and viscosity : 
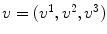 ).
).