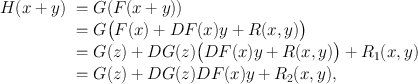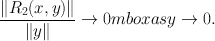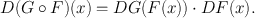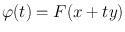Introduction
This chapter examines basic topics in the field of ordinary differential equations (ODE), as it has developed from the era of Newton into modern times. This is closely tied to the development of a number of concepts in advanced calculus. We begin with a brief discussion of the derivative of a vector-valued function of several variables as a linear map. We then establish in the fundamental local existence and uniqueness of solutions to ODE, of the form
where F ( t , y ) is continuous in both arguments and Lipschitz in y , and y takes values in k . The proof uses a nice tool known as the contraction mapping principle; next we use this principle to establish the inverse and implicit function theorems in .
The first six sections have a fairly purely analytic character and present ODE from a perspective similar to that seen in introductory courses. It is expected that the reader has seen much of this material before. Beginning in , this transition is complete. Appendix B, at the end of this volume, collects some of the basic facts about manifolds which are useful for such an approach to analysis.
Physics is a major source of differential equations, and in we study a general class of variational problems, giving rise to both the equations of mechanics and the equations of geodesics, all expressible in Hamiltonian form.
In .
Results on Hamiltonian systems are applied in gives a brief relativistic treatment of the equations of motion arising from the electromagnetic force, which ushered in Einsteins theory of relativity.
In can be found in Appendix C and in Chaps.5 and 10. Also the Brouwer fixed-point theorem will be extended to the LeraySchauder fixed-point theorem, and applied to problems in nonlinear PDE, in Chap.14.
The appendix at the end of this chapter discusses the existence and uniqueness of solutions to () when F satisfies a condition weaker than Lipschitz in y . Results established here are applicable to the study of ideal fluid flow, as will be seen in Chap.17.
The derivative
Let
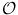
be an open subset of n , and let
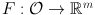
be a continuous function. We say that F is differentiable at a point
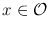
, with derivative L , if L : n m is a linear transformation such that, for small y n ,
with
We denote the derivative at x by DF ( x )= L . With respect to the standard bases of n and m , DF ( x ) is simply the matrix of partial derivatives,
so that, if
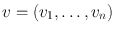
(regarded as a column vector), then
It will be shown that F is differentiable whenever all the partial derivatives exist and are continuous on
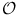
. In such a case we say that F is a C 1-function on
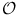
. In general, F is said to be C k if all its partial derivatives of order k exist and are continuous.
In () we can use the Euclidean norm on n and m . This norm is defined by
for
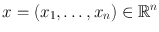
. Any other norm would do equally well. Some basic results on the Euclidean norm are derived in .
More generally, the definition of the derivative given by () extends to a function
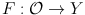
, where
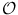
is an open subset of X , and X and Y are Banach spaces. Basic material on Banach spaces appears in Appendix A, Functional Analysis. In this case, we require L to be a bounded linear map from X to Y . The notion of differentiable function in this context is useful in the study of nonlinear PDE.
We now derive the chain rule for the derivative. Let
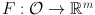
be differentiable at
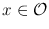
, as above; let U be a neighborhood of z = F ( x ) in m ; and let G : U k be differentiable at z . Consider H = G F . We have
with
Thus G F is differentiable at x , and
This result works equally well if n , m , and k are replaced by general Banach spaces.
Another useful remark is that, by the fundamental theorem of calculus, applied to
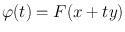














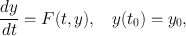
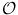 be an open subset of n , and let
be an open subset of n , and let 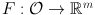 be a continuous function. We say that F is differentiable at a point
be a continuous function. We say that F is differentiable at a point 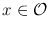 , with derivative L , if L : n m is a linear transformation such that, for small y n ,
, with derivative L , if L : n m is a linear transformation such that, for small y n , 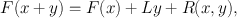
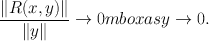
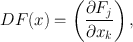
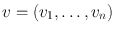 (regarded as a column vector), then
(regarded as a column vector), then 
 . In such a case we say that F is a C 1-function on
. In such a case we say that F is a C 1-function on 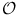 . In general, F is said to be C k if all its partial derivatives of order k exist and are continuous.
. In general, F is said to be C k if all its partial derivatives of order k exist and are continuous.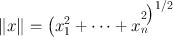
 . Any other norm would do equally well. Some basic results on the Euclidean norm are derived in .
. Any other norm would do equally well. Some basic results on the Euclidean norm are derived in .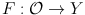 , where
, where 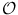 is an open subset of X , and X and Y are Banach spaces. Basic material on Banach spaces appears in Appendix A, Functional Analysis. In this case, we require L to be a bounded linear map from X to Y . The notion of differentiable function in this context is useful in the study of nonlinear PDE.
is an open subset of X , and X and Y are Banach spaces. Basic material on Banach spaces appears in Appendix A, Functional Analysis. In this case, we require L to be a bounded linear map from X to Y . The notion of differentiable function in this context is useful in the study of nonlinear PDE.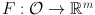 be differentiable at
be differentiable at 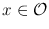 , as above; let U be a neighborhood of z = F ( x ) in m ; and let G : U k be differentiable at z . Consider H = G F . We have
, as above; let U be a neighborhood of z = F ( x ) in m ; and let G : U k be differentiable at z . Consider H = G F . We have