Volume 346
Springer Proceedings in Mathematics & Statistics
This book series features volumes composed of selected contributions from workshops and conferences in all areas of current research in mathematics and statistics, including operation research and optimization. In addition to an overall evaluation of the interest, scientific quality, and timeliness of each proposal at the hands of the publisher, individual contributions are all refereed to the high quality standards of leading journals in the field. Thus, this series provides the research community with well-edited, authoritative reports on developments in the most exciting areas of mathematical and statistical research today.
More information about this series at http://www.springer.com/series/10533
Editors
Shigeaki Koike
Department of Applied Physics, Waseda University, Tokyo, Japan
Hideo Kozono
Department of Mathematics, Waseda University, Tokyo, Japan
Takayoshi Ogawa
Mathematical Institute, Tohoku University, Sendai, Japan
Shigeru Sakaguchi
Graduate School of Information Sciences, Tohoku University, Sendai, Japan
ISSN 2194-1009 e-ISSN 2194-1017
Springer Proceedings in Mathematics & Statistics
ISBN 978-981-33-4821-9 e-ISBN 978-981-33-4822-6
https://doi.org/10.1007/978-981-33-4822-6
Mathematics Subject Classication (2010): 35D40 35J86 35K45 35K90 35Q30 58J50
Springer Nature Singapore Pte Ltd. 2021
This work is subject to copyright. All rights are reserved by the Publisher, whether the whole or part of the material is concerned, specifically the rights of translation, reprinting, reuse of illustrations, recitation, broadcasting, reproduction on microfilms or in any other physical way, and transmission or information storage and retrieval, electronic adaptation, computer software, or by similar or dissimilar methodology now known or hereafter developed.
The use of general descriptive names, registered names, trademarks, service marks, etc. in this publication does not imply, even in the absence of a specific statement, that such names are exempt from the relevant protective laws and regulations and therefore free for general use.
The publisher, the authors and the editors are safe to assume that the advice and information in this book are believed to be true and accurate at the date of publication. Neither the publisher nor the authors or the editors give a warranty, expressed or implied, with respect to the material contained herein or for any errors or omissions that may have been made. The publisher remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
This Springer imprint is published by the registered company Springer Nature Singapore Pte Ltd.
The registered company address is: 152 Beach Road, #21-01/04 Gateway East, Singapore 189721, Singapore
Preface
The proceedings contain several original surveys by invited speakers in a series of workshops entitled Partial Differential Equation and Future Applications, which was organized by Tohoku Forum for Creativity (TFC for short) supported in Tohoku University from July 2017 to October 2017, and also some research papers in related fields. The TFC program has started since 2013 and is evolving over various research fields on natural and human sciences. The above title Nonlinear Partial Differential Equations for Future Applications is one of the thematic programs in TFC. In our program, we focussed on nonlinear partial differential equations arising in fluid mechanics, reaction diffusion, optimal control, modern physics, material sciences, and geometry. Furthermore, in order to search for new applications, we invited experts from other areas.
Our program consists of the following workshops:
July 1014, 2017
Evolution Equations and Mathematical Fluid Dynamics
July 1721, 2017
Optimal Control and PDE
July 2428, 2017
Hyperbolic and Dispersive PDE
October 26, 2017
Geometry and Inverse Problems
in cooperation with A3 Foresight Program
The aim of this series of workshops was to introduce new and active fields of nonlinear partial differential equations (PDE for short) to young researchers, and moreover, to discover possibilities to connect related sciences with mathematics.
The purpose to publish these proceedings is, in addition, to enable the interested researchers to know valuable surveys with more detailed explanations. Moreover, we have decided to add several original papers which will be important contributions to future researches.
Editors
Shigeaki Koike
Hideo Kozono
Takayoshi Ogawa
Shigeru Sakaguchi
Tokyo, Japan Tokyo, Japan Sendai, Japan Sendai, Japan
Contents
Robert Denk
Yoshiyuki Kagei
Jishan Fan and Tohru Ozawa
Takayoshi Ogawa
Andrzej wich
Shigeaki Koike
A. Enciso , D. Peralta-Salas and F. Torres de Lizaur
Springer Nature Singapore Pte Ltd. 2021
S. Koike et al. (eds.) Nonlinear Partial Differential Equations for Future Applications Springer Proceedings in Mathematics & Statistics https://doi.org/10.1007/978-981-33-4822-6_1
An Introduction to Maximal Regularity for Parabolic Evolution Equations
Robert Denk
(1)
Department of Mathematics and Statistics, University of Konstanz, 78457 Konstanz, Germany
Abstract
In this note, we give an introduction to the concept of maximal 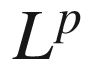 -regularity as a method to solve nonlinear partial differential equations. We first define maximal regularity for autonomous and non-autonomous problems and describe the connection to Fourier multipliers and
-regularity as a method to solve nonlinear partial differential equations. We first define maximal regularity for autonomous and non-autonomous problems and describe the connection to Fourier multipliers and  -boundedness. The abstract results are applied to a large class of parabolic systems in the whole space and to general parabolic boundary value problems. For this, both the construction of solution operators for boundary value problems and a characterization of trace spaces of Sobolev spaces are discussed. For the nonlinear equation, we obtain local in time well-posedness in appropriately chosen Sobolev spaces. This manuscript is based on known results and consists of an extended version of lecture notes on this topic.
-boundedness. The abstract results are applied to a large class of parabolic systems in the whole space and to general parabolic boundary value problems. For this, both the construction of solution operators for boundary value problems and a characterization of trace spaces of Sobolev spaces are discussed. For the nonlinear equation, we obtain local in time well-posedness in appropriately chosen Sobolev spaces. This manuscript is based on known results and consists of an extended version of lecture notes on this topic.
Keywords
Maximal regularity Fourier multipliers Parabolic boundary value problems Quasilinear evolution equations














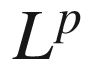 -regularity as a method to solve nonlinear partial differential equations. We first define maximal regularity for autonomous and non-autonomous problems and describe the connection to Fourier multipliers and
-regularity as a method to solve nonlinear partial differential equations. We first define maximal regularity for autonomous and non-autonomous problems and describe the connection to Fourier multipliers and  -boundedness. The abstract results are applied to a large class of parabolic systems in the whole space and to general parabolic boundary value problems. For this, both the construction of solution operators for boundary value problems and a characterization of trace spaces of Sobolev spaces are discussed. For the nonlinear equation, we obtain local in time well-posedness in appropriately chosen Sobolev spaces. This manuscript is based on known results and consists of an extended version of lecture notes on this topic.
-boundedness. The abstract results are applied to a large class of parabolic systems in the whole space and to general parabolic boundary value problems. For this, both the construction of solution operators for boundary value problems and a characterization of trace spaces of Sobolev spaces are discussed. For the nonlinear equation, we obtain local in time well-posedness in appropriately chosen Sobolev spaces. This manuscript is based on known results and consists of an extended version of lecture notes on this topic.