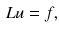1.1 Partial Differential Equations
Continuous phenomena, such as wave propagation or fluid flow, are generally modeled with partial differential equations (PDE), which express relationships between rates of change with respect to multiple independent variables. In contrast, phenomena that can be described with a single independent variable, such as the motion of a rigid body in classical physics, are modeled by ordinary differential equations (ODE).
A general PDE for a function u has the form
The order of this equation is m , the order of the highest derivative appearing (which is assumed to be finite). A classical solution u admits continuous partial derivatives up to order m and satisfies () at all points
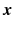
in its domain. In certain situations the differentiability requirements can be relaxed, allowing us to define weak solutions that do not solve the equation literally.
A somewhat subtle aspect of the definition () is the fact that the equation is required to be local . This means that functions and derivatives appearing in the equation are all evaluated at the same point.
Although classical physics provided the original impetus for the development of PDE theory, PDE models have since played a crucial role in many other fields, including engineering, chemistry, biology, ecology, medicine, and finance. Many industrial applications of mathematics are based on the numerical analysis of PDE.
Most PDE are not solvable in the explicit sense that a simple calculus problem can be solved. That is, we typically cannot obtain a exact formula for
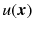
. Therefore much of the analysis of PDE is focused on drawing meaningful conclusions from an equation without actually writing down a solution.
1.2 Example: dAlemberts Wave Equation
One of the earliest and most influential PDE models was the wave equation , developed by Jean dAlembert in 1746 to describe the motion of a vibrating string. With physical constants normalized to 1, the equation reads
where u ( t , x ) denotes the vertical displacement of the string at position x and time t . If the string has length
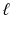
and is attached at both ends, then we also require that
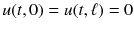
for all t . We will discuss the formulation of this model in Sect..
DAlembert also found a general formula for the solution of () is solved by any function of the form
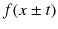
, assuming f is twice-differentiable. Given two such functions on
, we can write a general solution
A similar formula applies in the case of a string with fixed ends. If f is
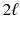
-periodic on
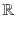
, meaning
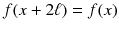
for all x , then it is easy to check that
satisfies
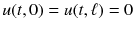
for any t .
One curious feature of this formula is that it appears to give a sensible solution even in cases where f is not differentiable. For example, to model a plucked string we might take the initial displacement to be a simple piecewise linear function in the form of a triangle from the fixed endpoints, as shown in Fig..
Fig. 1.1
Initial state of a plucked string
If we extend this to an odd,
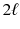
-periodic function on
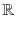
, then the formula (. The initial kink splits into two kinks which travel in opposite directions on the string and and appear to rebound from the fixed ends.
Fig. 1.2
Evolution of the plucked string, starting from
at the top
This is not a classical solution because u is not differentiable at the kinks. However, u does satisfy the requirements for a weak solution, as we will see in Chap..
Although a physical string could not exhibit sharp corners without breaking, the piecewise linear solutions are nevertheless physically reasonable. Direct observations of plucked and bowed strings were first made in the late 19th century by Hermann von Helmholtz, who saw patterns of oscillation quite similar to what is shown in Fig.. The appearance of kinks propagating along the string is striking, although the corners are not exactly sharp.
1.3 Types of Equations
There is no general theory of PDE that allows us to analyze all equations of the form (). To make progress it is necessary to restrict our attention to certain classes of equations and develop methods appropriate to those.
The most fundamental distinction between PDE is the property of linearity . A PDE is called linear if it can be written in the form
where f is some function independent of u , and L is a differential operator. Many of the important classical PDE that we will discuss in this book are linear and of first or second order. For such cases L has the general form














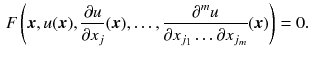
 in its domain. In certain situations the differentiability requirements can be relaxed, allowing us to define weak solutions that do not solve the equation literally.
in its domain. In certain situations the differentiability requirements can be relaxed, allowing us to define weak solutions that do not solve the equation literally.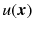 . Therefore much of the analysis of PDE is focused on drawing meaningful conclusions from an equation without actually writing down a solution.
. Therefore much of the analysis of PDE is focused on drawing meaningful conclusions from an equation without actually writing down a solution.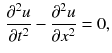
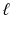 and is attached at both ends, then we also require that
and is attached at both ends, then we also require that 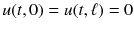 for all t . We will discuss the formulation of this model in Sect..
for all t . We will discuss the formulation of this model in Sect..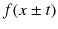 , assuming f is twice-differentiable. Given two such functions on
, assuming f is twice-differentiable. Given two such functions on 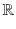 , we can write a general solution
, we can write a general solution 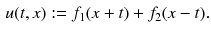
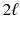 -periodic on
-periodic on  , meaning
, meaning 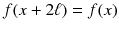 for all x , then it is easy to check that
for all x , then it is easy to check that 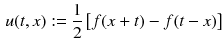
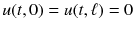 for any t .
for any t .
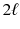 -periodic function on
-periodic function on  , then the formula (. The initial kink splits into two kinks which travel in opposite directions on the string and and appear to rebound from the fixed ends.
, then the formula (. The initial kink splits into two kinks which travel in opposite directions on the string and and appear to rebound from the fixed ends. 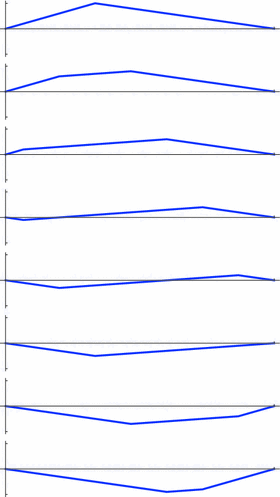
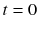 at the top
at the top