Introduction
In this chapter we discuss the basic theory of pseudodifferential operators as it has been developed to treat problems in linear PDE. We define pseudodifferential operators with symbols in classes denoted S , m , introduced by L. Hrmander. In 2 we derive some useful properties of their Schwartz kernels. In 3 we discuss adjoints and products of pseudodifferential operators. In 4 we show how the algebraic properties can be used to establish the regularity of solutions to elliptic PDE with smooth coefficients. In 5 we discuss mapping properties on L 2 and on the Sobolev spaces H s . In 6 we establish Grdings inequality.
In 7 we apply some of the previous material to establish the existence of solutions to hyperbolic equations. In 8 we show that certain important classes of pseudodifferential operators are preserved under the action of conjugation by solution operators to (scalar) hyperbolic equations, a result of Y. Egorov. We introduce the notion of wave front set in 9 and discuss the microlocal regularity of solutions to elliptic equations. We also discuss how solution operators to a class of hyperbolic equations propagate wave front sets. In 10 there is a brief discussion of pseudodifferential operators on manifolds.
We give some further applications of pseudodifferential operators in the next three sections. In 11 we discuss, from the perspective of the pseudodifferential operator calculus, the classical method of layer potentials, applied particularly to the Dirichlet and Neumann boundary problems for the Laplace operator. Historically, this sort of application was one of the earliest stimuli for the development of the theory of singular integral equations. One function of 11 is to provide a warm-up for the use of similar integral equations to tackle problems in scattering theory, in 7 of Chap. 9. Section 12Scattering by rough obstaclessection.9.12.1924 looks at general regular elliptic boundary problems and includes material complementary to that developed in 11 of Chap. 5. In 13 we construct a parametrix for the heat equation and apply this to obtain an asymptotic expansion of the trace of the solution operator. This expansion will be useful in studies of the spectrum in Chap. 8 and in index theory in Chap. 10.
In 14 we introduce the Weyl calculus. This can provide a powerful alternative to the operator calculus developed in 16, as can be seen in (Ho). Here we concentrate on identities, tied to symmetries in the Weyl calculus. We show how this leads to a quicker construction of a parametrix for the heat equation than the method used in 13. We will make use of this in 10 of Chap. 10, on a direct attack on the index theorem for elliptic differential operators on two-dimensional manifolds.
In 15, we study a class of pseudodifferential operators of Harmonic oscillator type. This class contains the Harmonic oscillator,
with symbol | x | 2 + | | 2, and results on these operators are interesting variants on those with symbols in S 1, 0 m .
Material in 110 is taken from Chap. 0 of (T).
The Fourier integral representation and symbol classes
Using a slightly different convention from that established in Chap. 3, we write the Fourier inversion formula as
where \hat{ f }() = (2) n f ( x ) e ix dx is the Fourier transform of a function on
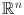
. If one differentiates (1.1), one obtains
where D = D 11 D n n , D j = (1 i ) x j . Hence, if
is a differential operator, we have
where
One uses the Fourier integral representation (1.3) to define pseudodifferential operators, taking the function p ( x , ) to belong to one of a number of different classes of symbols. In this chapter we consider the following symbol classes, first defined by Hrmander (Ho).
Assuming , [0, 1],
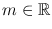
, we define S , m to consist of C -functions p ( x , ) satisfying
for all , , where = (1 + | | 2)1 2. In such a case we say the associated operator defined by (1.3) belongs to OPS , m . We say that p ( x , ) is the symbol of p ( x , D ). The case of principal interest is = 1, = 0. This class is defined by ().
Recall that in Chap. 3, 8, we defined
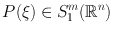
to satisfy (1.4), with = 1, and with no x -derivatives involved. Thus S 1, 0 m contains
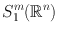
.
If there are smooth p m j ( x , ), homogeneous in of degree m j for | | 1, that is, p m j ( x , r ) = r m j p m j ( x , ) for r , | | 1, and if
in the sense that















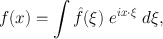
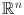 . If one differentiates (1.1), one obtains
. If one differentiates (1.1), one obtains 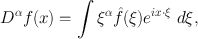
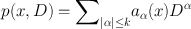
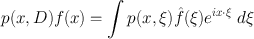
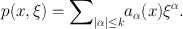
 , we define S , m to consist of C -functions p ( x , ) satisfying
, we define S , m to consist of C -functions p ( x , ) satisfying 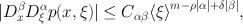
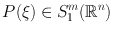 to satisfy (1.4), with = 1, and with no x -derivatives involved. Thus S 1, 0 m contains
to satisfy (1.4), with = 1, and with no x -derivatives involved. Thus S 1, 0 m contains 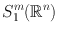 .
.