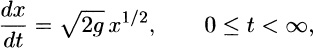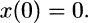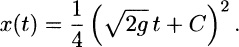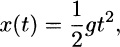EXAMPLE 2.
Consider the IVP
(4) 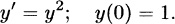
Here, f(x, y) = y2 and f/y = 2y are continuous everywhere in the x, y plane, so assures us that there is a unique solution of the IVP (4) in some interval about the initial point.
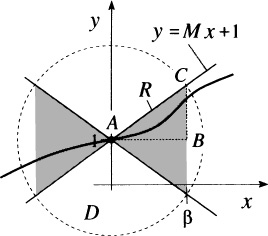
Interval of existence and uniqueness in Example 2.
What we can learn (without peeking at the solution, as we did in Example 1) about the interval of existence and uniqueness of that solution? [Actually, (4) can be solved readily by separation of variables, but let us see what we can determine even in the absence of having the solution in hand to examine.]
Since the continuity conditions are satisfied throughout the plane, we can make the disk D any size we like. Begin by drawing the disk D, of radius R, about the initial point (0,1), as in . Everywhere in D, |y| = |y2| < (R + 1)2 because the maximum y is at the top of the disk, where y = R: + 1. Thus, the absolute magnitude of the slope of the solution curve through (0,1) is less than (R + 1)2, which we will denote as M, so the solution curve must fall within the shaded bow tie region. After all, for the solution curve to break out of the bow tie its slope would have to exceed M at the point of break out, and that cannot happen because |y| < M everywhere in D.
Hence, the interval of existence and uniqueness is at least < x < . To determine , write the Pythagorean theorem for the right triangle ABC: AB2 + BC2 = R2 or, 2 + (M)2 = R2, which can be solved for as
(5) 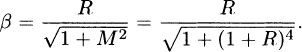
For instance, R = 1 gives = 0.2425. Since we can choose R as large or small as we like, we might as well choose R so as to maximize the right hand side of (5). To do that, set d/dR = 0 and obtain R4 + 2R3 2R 2 = 0 which (using computer software) gives R = 1.1069; putting that into (5) then gives = 0.2031. Thus, we have shown that the interval of existence and uniqueness is at least 0.2031 < x < 0.2031.
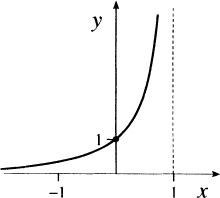
In fact, (4) is readily solved, its solution being
(6) 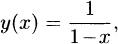
The exact solution (6) of the IVP (4).
the graph of which is given in . Thus, the actual interval of existence and uniqueness is < x < 1, so the interval 0.2031 < x < 0.2031 is correct, but falls well short of capturing the full interval of existence. 
1.5.3 Application to free fall; physical significance of nonuniqueness
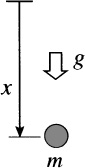
It is important to give a physical application as well, so the impression is not left that the questions of existence and uniqueness are only of theoretical interest. Such an application can be found even in the simple problem of a body of mass m that is dropped from rest at time t = 0. Let the masss downward displacement from the point of release be x(t) (). Neglecting air resistance, Newtons second law gives mx = mg, so we have the IVP
Free fall under the influence of gravity, neglecting air resistance.
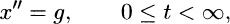
(7b) 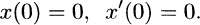
We can integrate (7a) twice with respect to t and use the initial conditions in (7b) influence of gravity, neglecting to evaluate the two constants of integration. Doing so gives the solution
(8) 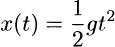
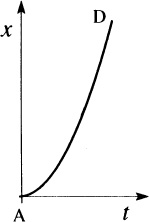
that is probably familiar from a first course in physics. The graph of (8) is the parabola shown in .
However, it will be instructive to work not with Newtons second law but with an energy equation. To derive an energy equation, multiply Newtons law mx = mg not by dt but by dx:
The solution x(t) = gt2/2 of (6).
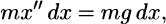
(9b) 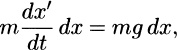
(9c) 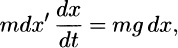
(9d) 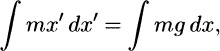
(9e) 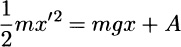
or 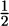 mx2 + (mgx) A. The latter is a statement of conservation of energy: The kinetic energy mx2/2 plus the (gravitational) potential energy mgx is a constant. Putting t = 0 in (9e) gives 0 = 0 + A so A = 0, and it follows from (9e) that x =
mx2 + (mgx) A. The latter is a statement of conservation of energy: The kinetic energy mx2/2 plus the (gravitational) potential energy mgx is a constant. Putting t = 0 in (9e) gives 0 = 0 + A so A = 0, and it follows from (9e) that x = 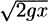 . The latter is a first-order differential equation, so append the single initial condition x(0) = 0. Then we have the IVP
. The latter is a first-order differential equation, so append the single initial condition x(0) = 0. Then we have the IVP
We say that (9e) is a first integral of (7a). In place of the second-order . Our starting point is now the IVP(10), not (7).
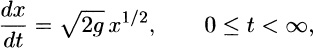
(10b) 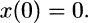
Our interest here is in considering the IVP (10) in the light of . Solve (10a) by separation of variables. If x 0 we can divide both sides by x1/2, multiply by dt, integrate, and obtain
(11) 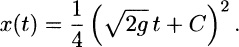
Then the initial condition x(0) = 0 gives C = 0 so
(12) 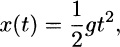
Next page










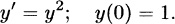
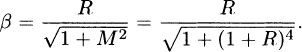
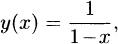

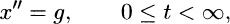
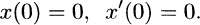
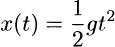
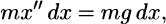
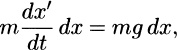
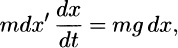
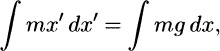
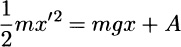
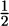 mx2 + (mgx) A. The latter is a statement of conservation of energy: The kinetic energy mx2/2 plus the (gravitational) potential energy mgx is a constant. Putting t = 0 in (9e) gives 0 = 0 + A so A = 0, and it follows from (9e) that x =
mx2 + (mgx) A. The latter is a statement of conservation of energy: The kinetic energy mx2/2 plus the (gravitational) potential energy mgx is a constant. Putting t = 0 in (9e) gives 0 = 0 + A so A = 0, and it follows from (9e) that x = 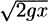 . The latter is a first-order differential equation, so append the single initial condition x(0) = 0. Then we have the IVP
. The latter is a first-order differential equation, so append the single initial condition x(0) = 0. Then we have the IVP