Greenberg - Solutions Manual to Accompany Ordinary Differential Equations

Copyright 2012 by John Wiley & Sons, Inc. All rights reserved.

Published by John Wiley & Sons, Inc., Hoboken, New Jersey.

Published simultaneously in Canada.

No part of this publication may be reproduced, stored in a retrieval system or transmitted in any form or by any means, electronic, mechanical, photocopying, recording, scanning or otherwise, except as permitted under Section 107 or 108 of the 1976 United States Copyright Act, without either the prior written permission of the Publisher, or authorization through payment of the appropriate per-copy fee to the Copyright Clearance Center, Inc., 222 Rosewood Drive, Danvers, MA 01923, (978) 750-8400, fax (978) 750-4470, or on the web at www.copyright.com. Requests to the Publisher for permission should be addressed to the Permissions Department, John Wiley & Sons, Inc., 111 River Street, Hoboken, NJ 07030, (201) 748-6011, fax (201) 748-6008, or online at http://www.wiley.com/go/permission.

Limit of Liability/Disclaimer of Warranty: While the publisher and author have used their best efforts in preparing this book, they make no representation or warranties with respect to the accuracy or completeness of the contents of this book and specifically disclaim any implied warranties of merchantability or fitness for a particular purpose. No warranty may be created or extended by sales representatives or written sales materials. The advice and strategies contained herein may not be suitable for your situation. You should consult with a professional where appropriate. Neither the publisher nor author shall be liable for any loss of profit or any other commercial damages, including but not limited to special, incidental, consequential, or other damages.

For general information on our other products and services please contact our Customer Care Department within the United States at (800) 762-2974, outside the United States at (317) 572-3993 or fax (317) 572-4002.

Wiley also publishes its books in a variety of electronic formats. Some content that appears in print, however, may not be available in electronic formats. For more information about Wiley products, visit our web site at www.wiley.com.

Library of Congress Cataloging-in-Publication Data:

Greenberg, Michael D.

Ordinary differential equations / Michael D. Greenberg.

p. cm.

Includes bibliographical references and index.

ISBN 978-1-118-39899-9

1. Differential equationsTextbooks. 2. Differential equations, PartialTextbooks. I. Title.

QA372.G725 2012

515'.352dc232011042287

This first section is simply to introduce you to differential equations: what they look like, some ideas as to how they arise in applications, and some important definitions. We see that the complete problem might be not just the differential equation, but also one or more "initial conditions." If such conditions are prescribed, the problem is called an initial value problem, or IVP. For instance, (6) [that is, equation (6) in the text] is an IVP because in addition to the DE (differential equation) there are two initial conditions, given by (6b), so that the solution of the IVP must satisfy not only the DE (6a), but also those two initial conditions.

Chapter 1 is about first-order equations; that is, equations in which the highest derivative is of first order. In that case, hence all through Chapter 1, there will be only one initial condition. In later chapters we will find that the "appropriate" number of initial conditions for a DE is the same as the order of the equation. For instance, (6a) is of second order and, sure enough, there are two initial conditions in (6b).

The distinction between linear and nonlinear differential equations will be of great importance, so it is necessary to be able to tell if a given equation is linear or nonlinear. Later, we will find that the key is whether or not a certain linearity property is satisfied, but for now it will suffice not to know about that property, but simply to say that an nth-order equation is linear if it is in, or can be put into, the form (14). What is the form of (14)? First, put all occurrences of the unknown, that is, the dependent variable such as y in (14), on the LHS (left-hand side of the equation); anything else goes on the right. If the LHS is a linear combination of y, y',, y(n), then the DE is linear. Actually, the "constants" that multiply y, y',, y(n) in (14) are permitted to be functions of x; the point is that they don't depend on y or its derivatives.

Example 1. (Definitions) State the order of the

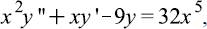
whether it is linear or nonlinear, homogeneous or nonhomogeneous, and determine whether or not the given functions are solutions, that is, whether or not they "satisfy" the DE:

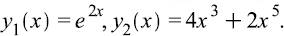
SOLUTION. The equation is of second order because the highest derivative present is of second order; it is linear because it is of the form (14), with a0(x) = x2, a1(x) = x, a2(x) = 9, and f(x) = 32x5; and it is nonhomogeneous because the RHS, 32x5 is not zero. The RHS does happen to be 0 at x = 0, but the equation is nonhomogeneous because the RHS is not identically zero on the interval under consideration. [Actually, we did not specify an x interval. The default interval is (-, ). Getting back to this example, surely x2 is not identically zero on (-, ).]

Now test y1(x) = ex to see if it is a solution of the DE. Simply substitute it into the equation and see if the equation is there by reduced to an identity, such as 6x + 3 sin x = 6x + 3 sin x. Inserting y1(x), gives x2(4e2x) + x(2e2x) -9e2 = 32x5, or (4x2 + 2x -9) e2x= 32x5. Surely, the latter is not identically true. How do we know that? Hopefully, we can just look at it and see that there is "no way" a quadratic in x times an exponential function of x can equal a multiple of a power of x. At the least we can use "brute force" and check the values of the LHS and RHS at one or more x's. For instance, a convenient point to use is x = 0, and there the LHS is -9 whereas the RHS is 0. Thus, y1(x) is not a solution of the DE.

Now test y2(x) = 4x3 + 2x5. This time, putting the latter into the DE gives, after some canceling of terms, 32x5 = 32x5 which is an identity. Thus, y2(x) is indeed a solution of the DE.

Now suppose we append to the DE these initial conditions at x = 0 : y(0) = 0, y'(0) = 0. y2(x) does satisfy these conditions, so it is a solution of the IVP consisting of the DE and the two given initial conditions. If the initial conditions were y(0) = 0 and y'(0) = 3, say, instead, then