Royal Eugene Collins - Mathematical Methods for Physicists and Engineers

Second Corrected Edition Royal Eugene Collins DOVER PUBLICATIONS, INC. Mineola, New York Copyright Copyright 1968, 1999 by Royal Eugene Collins All rights reserved under Pan American and International Copyright Conventions. Bibliographical Note This Dover edition, first published in 1999, is an unabridged and corrected republication of the first edition of Mathematical Methods for Physicists and Engineers published by Reinhold Book Corporation in 1968. Library of Congress Cataloging-in-Publication Data Collins, Royal Eugene. Mathematical methods for physicists and engineers / Royal Eugene Collins. ed. p. cm. cm.

Includes bibliographical references and index. eISBN 978-0-486-15012-3 (pbk.) 1. Mathematics. 2. Mathematical physics. 3.

Engineering mathematics. I. Title. QA37.2.C656 1999 510dc21 98-28913
CIP Manufactured in the United States of America
Dover Publications, Inc., 31 East 2nd Street, Mineola, N.Y. 11501

In preparing this text I have drawn heavily on a great number and variety of texts on applied mathematics. Many are cited as desirable references for the student.

I am indebted to all of these authors as my teachers. I am also indebted to my students over the years who, by their responses, have taught me how to teach this material in a more effective way each year. I express my appreciation to Mrs. Gloria Parr and Mrs. Shirley Double for their patience with my poor handwriting in typing this manuscript, and to my son, Mr. R.E.C.

The physical sciences and engineering have become increasingly mathematical during the 20th century, and indeed the same trend is also observed in the biological sciences. The physical sciences and engineering have become increasingly mathematical during the 20th century, and indeed the same trend is also observed in the biological sciences.

Advanced undergraduates, or beginning graduate students, in these fields find themselves in need of a certain mathematical tools in order to comprehend the physical principles, and their applications, encountered in their major courses. Here we emphasize mathematical tools rather than mathematics because the student of physics or engineering must use these elements of mathematics as tools to achieve the desired understanding of the physics rather than simply comprehend the mathematics itself. This distinction is important. The mathematical tools most urgently needed, beyond a one-semester course in ordinary differential equations, as offered in the mathematics departments of most colleges and universities, are as follows: a knowledge of vector calculus, matrix algebra, and linear vector operations; the many and varied methods of solving linear boundary value problems, including a good familiarity with the more common special functions of mathematical physics; some knowledge of the calculus of variations, and variational and perturbation approximations applicable to boundary value problems and nonlinear differential equations; the ability to evaluate complicated integrals, or sum series; a facility for curve fitting and numerical approximation methods; a familiarity with the basic elements or probability and how these apply to physical problems; and, finally, some knowledge of integral equations. This is a formidable list, and if the student were to try to completely master these many areas form the mathematicians point of view, it would be more than a lifetime task. However, the essential needs of the student can be met without such complete mastery.

Most universities attempt to meet this need with a one-year course in the mathematics department, usually called Mathematics for Engineers and Physicists and commonly taught in the students junior year. However, rarely is even a small part of the above list actually treated in the course. As a result, a great amount of time must usually be devoted to the teaching of mathematics in each and every course in physics or engineering. This situation exists partially as a result of the form of most texts available for such a course and partially because of the method of presentation in the mathematics class. The text presented here is intended to help remedy this situation in two ways: first, by including an adequate treatment of all the needed topics in applied mathematics; and second by presenting the material in the form of programmed instruction. The text has been designed to be entirely readable so that the material can be comprehended by advanced undergraduate, or beginning graduate, students without any assistance from the instructor.

Consequently, class time can be devoted almost entirely to reviewing the problems executed by the student, thus dispensing with formal lectures on the mathematical methods. It is recommended that the student be assigned a segment to read along with a corresponding set of problems to solve. These can then be reviewed and discussed in the following class session. Occasionally, the instructor may find it necessary to work out some of the more difficult problems or to enlarge on a particular topic with additional examples. Further, some of the text segments and problems sets are rather long and may require two or three class sessions to cover adequately. Nevertheless, it should be possible to cover all of this text in two semesters if this method of teaching is used.

The author has found it to be most effective over a period of several years using essentially the material of this text as prepared notes issued to students. Some of my mathematician friends may question the lack of rigor in this text, but they must remember the objective of the text and forgive me. The intent is to eliminate most of this same material from present physics and engineering courses by putting all of it into one course. The mathematician may wish to call the course something other than Mathematics; I prefer Mathematical Tools. This compaction of applied topics will also leave physics and engineering students free to include in their curricula additional courses in pure mathematics, subjects such as point set theory, topology, and others that are strongly recommended, especially for physics students. In addition, this method will allow students to concentrate on physics, or engineering, in their major courses.

The end result is that courses in physics and engineering will be stronger, and students better educated. R. E. Collins

Here we present a brief but essentially complete presentation of those elements of vector calculus essential for the physicist or engineer. A knowledge of the elementary algebra of vectors is assumed. 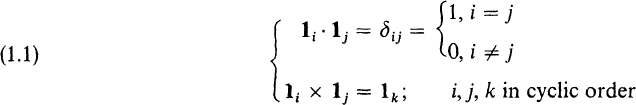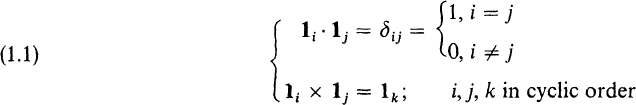We consider a point in space defined with reference to a set of rectangular cartesian coordinates by the three numbers, x1, x2, x3, which are the coordinates of the point, or the orthogonal projections of the point, on the three Then we write,