MATLAB perfectly handlessymbolic mathematical computations, manipulating and performing operations onformulae and algebraic expressions with ease.
1.2 Symbolic computation with MATLAB
MATLAB perfectly handlessymbolic mathematical computations, manipulating and performing operations onformulae and algebraic expressions with ease.
You can expand, factor andsimplify polynomials and rational and trigonometric expressions, find algebraicsolutions of polynomial equations and systems of equations, evaluatederivatives and integrals symbolically, find solutions of differentialequations, manipulate powers, and investigate limits and many other features ofalgebraic series. To perform these tasks,MATLAB first requires all the variables (or algebraic expressions) to bewritten between single quotes. When MATLAB receives a variable or expression inquotes, it is interpreted as symbolic. Here are some examples ofsymbolic computations with MATLAB. 1) We can expand thefollowing algebraic expression: ((x + 1)(x+2)-(x+2) ^2)^3. This is done by typing: expand('((x + 1)(x+2)-(x+2) ^ 2) ^ 3').
Theresult will be another algebraic expression: syms x; expand(((x + 1) *(x + 2)-(x +2) ^ 2) ^ 3)ans =-x ^ 3-6 * x ^ 2-12 * x-8 2) We can factor the resultof the calculation in the above example by typing: factor('((x + 1) *(x + 2)-(x+ 2) ^ 2) ^ 3') syms x; factor(((x + 1)*(x + 2)-(x +2)^2)^3)ans =-(x+2)^3 3) We can find theindefinite integral of the function (x ^ 2) sin(x) ^ 2 by typing:int('x ^ 2 * sin(x) ^ 2', 'x') int('x^2*sin(x)^2', 'x')ans =x ^ 2 *(-1/2 * cos(x) * sin(x) + 1/2 * x)-1/2 * x* cos(x) ^ 2 + 1/4 * cos(x) * sin(x) + 1/4 * 1/x-3 * x ^ 3 4) We can simplify the previous result: >> syms x;simplify(int(x^2*sin(x)^2, x))ans =sin(2*x)/8 -(x*cos(2*x))/4 -(x^2*sin(2*x))/4 +x^3/6 5) We can present the previous result using a moreelegant mathematical notation: >> syms x;pretty(simplify(int(x^2*sin(x)^2, x)))ans =2 3sin(2 x) x cos(2 x) x sin(2 x) x-------- ----------- - ----------- + --8 4 4 6 6) We can find the seriesexpansion up to order 12 of the function x ^ 2 * sin (x) ^ 2, presenting theresult in elegant form: pretty(taylor('x^2*sin(x)^2',12)) 4 6 8 10 12 x - 1/3 x + 2/45 x - 1/315 x + o (x) 7) We can solve theequation 3ax-7 x ^ 2 + x ^ 3 = 0 (where a is aparameter): solve('3*a*x-7*x^2 + x^3 = 0', 'x')ans =[ 0][7/2 + 1/2 *(49-12*a) ^(1/2)][7/2-1/2 *(49-12*a) ^(1/2)] 8) We can find the fivesolutions of the equation x ^ 5 + 2 x + 1 = 0: solve('x^5+2*x+1','x')ans =RootOf(_Z^5+2*_Z+1) As the result does not explicitlygive five solutions, we apply the "allvalues" command: allvalues(solve('x^5+2*x+1','x'))ans =[-.7018735688558619-. 8796971979298240* i][-. 7018735688558619 +.8796971979298240 * i][-. 4863890359345430][.9450680868231334-. 8545175144390459 *i][. 8545175144390459* i] On the other hand, MATLABcan use the Maple program libraries to work with symbolic math, and can thusextend its field of action. 8545175144390459* i] On the other hand, MATLABcan use the Maple program libraries to work with symbolic math, and can thusextend its field of action.
In this way, MATLAB can be used to work on suchtopics as differential forms, Euclidean geometry, projective geometry,statistics, etc. At the same time, Maple canalso benefit from MATLABs powers of numerical calculation, which might beused, for example, in combination with the Maple libraries (combinatorics,optimization, number theory, etc.)
1.3 MATLAB and Maple
Provided the "Extended SymbolicMath Toolbox" is installed then MATLAB can extend its symbolic calculationabilities by making use of the Maple libraries. To use a Maple command fromMATLAB, use the command 'maple' followed by the corresponding Maple syntax. To use a Maple command fromMatlab, the syntax is as follows:
maple('Maple_command_syntax') or alternatively:
maple'Maple_command_syntax' To use a Maple command withN arguments from Matlab, the syntax is as follows:
maple('Maple_command_syntax',argument1,argument2,...,argumentN) Here are some examples. 1) We can calculate thelimit of the function (x ^ 3-1) / (xs) as x tends to 1:
maple('limit((x^3-1)/(x-1),x=1)') ans= We could also have used thefollowing syntax:
maple limit('(x^3-1)/(x-1),x=1)'; ans= 2) We can calculate thegreatest common divisor of 10,000 and 5,000:
maple('gcd', 10000, 5000) ans = 5000
1.4 Graphics with MATLAB
MATLAB can generate two-and three-dimensional graphs, as well as contour and density plots. You cangraphically represent data lists, controlling colors, shading and othergraphics features.
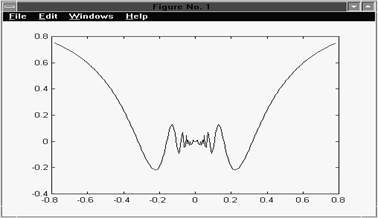
Animated graphics are also supported. Graphics produced byMATLAB are portable to other programs. Some examples of MATLABgraphics are given below. 1) We can represent thefunction xsin(1/x) for x ranging between - p /4 and p /4,taking 300 equidistant points in the interval. See Figure 1-1. x = linspace(-pi/4,pi/4,300);y=x.*sin(1./x);plot(x,y)