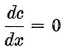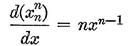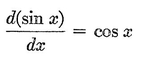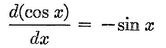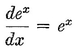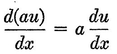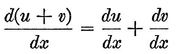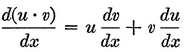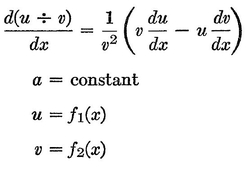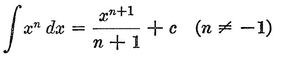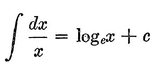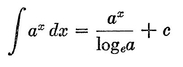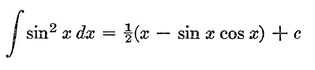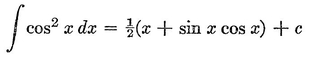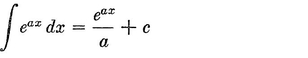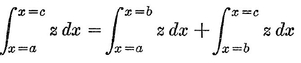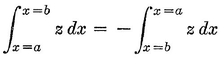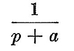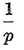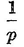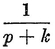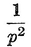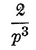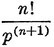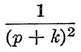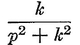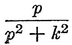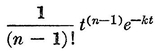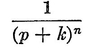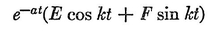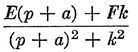Ritow - Capsule Calculus
Here you can read online Ritow - Capsule Calculus full text of the book (entire story) in english for free. Download pdf and epub, get meaning, cover and reviews about this ebook. year: 2013, publisher: Dover Publications;INscribe Digital, genre: Children. Description of the work, (preface) as well as reviews are available. Best literature library LitArk.com created for fans of good reading and offers a wide selection of genres:
Romance novel
Science fiction
Adventure
Detective
Science
History
Home and family
Prose
Art
Politics
Computer
Non-fiction
Religion
Business
Children
Humor
Choose a favorite category and find really read worthwhile books. Enjoy immersion in the world of imagination, feel the emotions of the characters or learn something new for yourself, make an fascinating discovery.
Capsule Calculus: summary, description and annotation
We offer to read an annotation, description, summary or preface (depends on what the author of the book "Capsule Calculus" wrote himself). If you haven't found the necessary information about the book — write in the comments, we will try to find it.
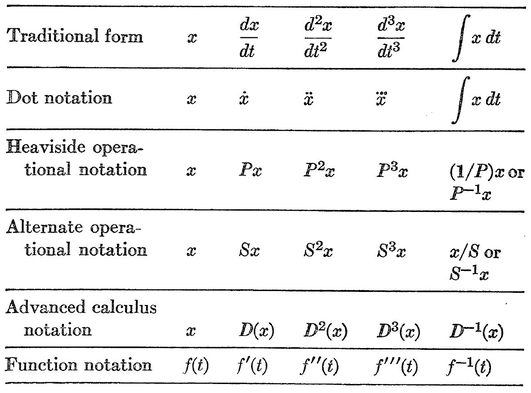
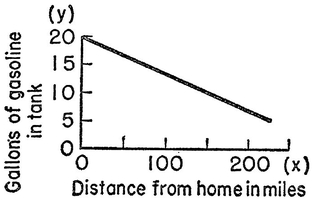
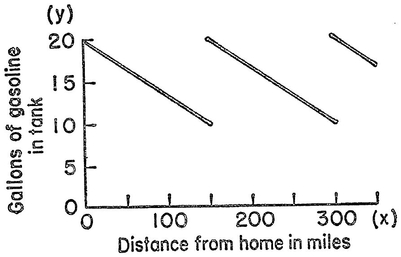
Abstract: This brief introductory text presents the basic principles of calculus from the engineering viewpoint. Excellent either as a refresher or as an introductory course, it focuses on developing familiarity with the basic principles rather than presenting detailed proofs. Topics include differential calculus, in terms of differentiation and elementary differential equations; integral calculus, in simple and multiple integration forms; time calculus; equations of motion and their solution; complex variables; complex algebra; complex functions; complex and operational calculus; and simple and inverse transformations. Advanced subjects comprise integrations and differentiation techniques, in addition to a more sophisticated variety of differential equations than those previously discussed. It is assumed that the reader possesses an acquaintance with algebra and trigonometry as well as some familiarity with graphs. Additional background material is presented as needed
Ritow: author's other books
Who wrote Capsule Calculus? Find out the surname, the name of the author of the book and a list of all author's works by series.
Capsule Calculus — read online for free the complete book (whole text) full work
Below is the text of the book, divided by pages. System saving the place of the last page read, allows you to conveniently read the book "Capsule Calculus" online for free, without having to search again every time where you left off. Put a bookmark, and you can go to the page where you finished reading at any time.
Font size:
Interval:
Bookmark:
TABLE I
SOME BASIC DERIVATIVES
 | ( e is any constant) |
 | |
 | |
 | |
 |
TABLE II
DERIVATIVES OF INVOLVED EXPRESSIONS
| Rule 1. |  |
| Rule 2. |  |
| Rule 3. |  |
| Rule 4. |  |
COMMONLY USED DERIVATIVES
 |
 |
 |
| ex dx = ex + c |
| sin x dx = cos x + e |
| cos x dx = sin x + e |
 |
 |
 |
| x is a variable; n is an integers; c and a are numbers. |
TABLE IV
LAWS OF INTEGRALS
| Rule 1. | az dx = a z dx |
| Rule 2. | (z + y) dx = z dx + y dx |
| Rule 3. |  |
| Rule 4. |  |
| Symbols x, y , and z are variables. a is a number. |
TABLE V
COMMONLY USED SYMBOLS FOR DIFFERENTIATION AND INTEGRATION WITH RESPECT TO TIME
ELEMENTARY LAPLACE TRANSFORMS
| Real Quantity | Transformed Quantity |
|---|---|
| V 2 | V 2 p , |
| V 2 | pV 2 p V 2(0) |
| 1 | 1/ p |
| t | 1/ p 2 |
| e at |  |
TABLE VII
LAPLACE TRANSFORMS
| Time Function ( x ) | Laplace transform ( X ) |
| 1 |  |
| unit step at t=0+ |  |
| e kt |  |
| t |  |
| t 2 |  |
| tn |  |
| te kt |  |
| sin kt |  |
| cos kt |  |
 |  |
 |  |
TABLE VIII
LAPLACE TRANSFORM THEOREMS
DEFINITIONS: Assume that x and y are related numbers with some physical meaning. For example, x might be the distance driven by a car and y the amount of gas in the gas tank.
As shown in , for every value of x there exists a value of y . This can also be stated as: y is a function of x [sometimes abbreviated as y = f ( x )]. With but a single value of y for every value of x in this case, it can be said that y is a single valued function of x . If for every value of x there were two or more possible values of y , the statement of their relationship would be: y is a multiple-valued function of x . If y is a single-valued function of x , then x may or may not also be a single-valued function of y.
In plotting the relationship between distance and gasoline for a long trip, such as shown in , x is a multiple-valued function of y.
Font size:
Interval:
Bookmark:
Similar books «Capsule Calculus»
Look at similar books to Capsule Calculus. We have selected literature similar in name and meaning in the hope of providing readers with more options to find new, interesting, not yet read works.
Discussion, reviews of the book Capsule Calculus and just readers' own opinions. Leave your comments, write what you think about the work, its meaning or the main characters. Specify what exactly you liked and what you didn't like, and why you think so.