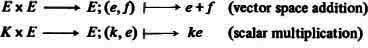Michael J. Field - Differential Calculus and Its Applications

DIFFERENTIAL

CALCULUS

AND

ITS APPLICATIONS

Michael J. Field

University of Houston

Dover Publications, Inc.

Mineola, New York

Copyright

Copyright 1976 by M. J. Field

All rights reserved.

Bibliographical Note

This Dover edition, first published in 2012, is an unabridged republication of the work originally published in 1976 by the Van Nostrand Reinhold Company Limited, New York and London.

Library of Congress Cataloging-in-Publication Data

Field, Mike.

Differential calulus and its applications / Michael J. Field. Dover ed.

p. cm.

Originally published: New York : Van Nostrand Reinhold, 1976.

Summary: This text offers a synthesis of theory and application related to modern techniques of differentiation. Based on undergraduate courses in advanced calculus, the treatment covers a wide range of topics, from soft functional analysis and finite-dimensional linear algebra to differential equations on submanifolds of Euclidean space. 1976 edition Provided by publisher.

Includes bibliographical references and index.

ISBN-13: 978-0-486-49795-2 (pbk.)

ISBN-10: 0-486-49795-X (pbk.)

1. Differential calculus. I. Title.

QA304.F5 2012

515.33dc23

2012020148

Manufactured in the United States by Courier Corporation

49795X01

www.doverpublications.com

2.2 o-notation

My primary concern in writing this book about several-variable differential calculus has been to achieve a synthesis of theory and application in the framework of the modern approach to differentiation as expounded in Dieudonns treatise on the Foundations of Modern Analysis. By application I mean here not only a working knowledge and familiarity with the techniques of differentiation but also applications of the theory to applied mathematics and other areas of pure mathematics, notably differential topology and differential equations.

The text is based on undergraduate courses on advanced calculus that I have taught at the Universities of Minnesota and Warwick and covers a fairly wide range-from soft functional analysis and finite-dimensional linear algebra to differential equations on submanifolds of Euclidean space. I hope that the book will not only be suitable for the final two years of an undergraduate degree course in pure or applied mathematics but will also form a suitable basis for graduate level courses on advanced calculus and differential manifolds.

In Chapter 2 we give a systematic exposition of the elementary theory of differentiation on normed vector spaces. Stress is laid on examples of differentiable functions defined on open subsets of Euclidean space. There are sections on extrema, curves in Rn, various forms of Taylors theorem and higher derivatives.

More advanced topics in the theory of differentiation are covered in Chapter 3. Among these are the inverse-function theorem, implicit-function theorem and the rank theorem. In the final section of this chapter, coordinate transformations are discussed together with applications to the solution of partial differential equations.

The final chapter is intended both as a consolidation of the theory given in the preceding chapters and as an introduction to differential manifolds and differential equations. The key results of Chapters 2 and 3 are repeatedly used in this chapter. Critical point theory, differential structures, submanifolds of Euclidean space, orientation of hypersurfaces, vector fields, tangent spaces and bundles are among the topics discussed.

Finally, one or two remarks about notation. The derivative of a map f: E F at x will be denoted by Dfx (not Df(x)) and will be a linear map from E to F. The value of Dfx at e E will be denoted by Dfx(e) (not Df(x)(e)). Arbitrary functions will be denoted by f, g, h, but linear maps will usually be denoted by capitals S, T, U, We write the composition of the functions g and f by gf but the composition of the linear maps S and T by S .T. This dot notation is expanded considerably in the text; suffice it to say that its use helps simplify many computations and formulae. For typographical convenience and clarity of exposition I have adopted the notation f;j(x) to mean the jth partial derivative of f at x. These, and other conventions, are explained more fully in the text.

September, 1975

M. J. FIELD

In this section we shall make a brief survey of that part of the elementary theory of vector spaces and linear maps that will be assumed in the rest of the text. For more detailed expositions we refer the reader to any of the many basic texts on linear algebra and finite-dimensional vector spaces (Halmos [9] is particularly recommended).

The symbol K will always be used to denote a field which, in practice, will either be R (the real numbers) or C (the complex numbers). The identity element of K will be denoted by 1 and the zero by 0.

Definition 0.1.1

A vector space over the field K consists of a set E, with distinguished element 0E, together with operations

such that the following conditions are satisfied.

1. The set E forms an Abelian group under + with zero element 0E

(a) e + f = f + e for all e, f E.

(b) e + (f + g) = (e + f) + g for all e, f, g E.

(c) e + 0E = 0E + e for all e E.

(d) For every e E, there exists a unique element e E such that e + (e) = 0E.

2. k(e + f) = ke + kf for all e, f E and k K.

3. (k + l)e = ke + le for all k, l K and e E.

4. k(le) = (kl)e, for all k, l K and e E.

5. le = e for all e E.

We shall denote a vector space by the symbol used for its underlying set. Thus, in the definition, the vector space would be denoted by E. In the sequel we shall usually denote the zero element of E by 0, as opposed to 0E. Thus we shall write 0e = 0 rather than 0e = 0E. We shall also often omit reference to the underlying field of scalars as it will generally remain fixed during the course of discussion.

We recall the definition of a vector subspace.

Definition 0.1.2

A subset F of the vector space E is said to be a vector subspace of E if the restriction of the vector space operations of E to F induces on F the structure of a vector space.

Remark. In order that F be a vector subspace of E it is clearly necessary and sufficient that

(a) F is closed under addition: e + f F for all e, f F.

(b) F is closed under scalar multiplication: ke F for all k K and e F.

The basic objects of study in the theory of vector spaces are linear maps, and we recall their definition.

Definition 0.1.3

Let E and F be vector spaces over the field K and let T : E F be a function from E to F. We call T a linear map or linear homomorphism (strictly, a K-linear map or K-linear homomorphism) if the following condition is satisfied for all e, f E and k K:

T(ke + f) = kT(e) + T(f)

Associated with a linear map T : E F we have the following vector spaces:

The kernel of T, Ker T, defined by Ker T = {e E: T(e) = 0}.

The image of T, Im T, defined by Im T = {f F: e E with T(e) = f}.

The cokernel of T, Coker T, defined by Coker T = F/Im T.

Ker T is a vector subspace of E and Im T is a vector subspace of F.