Calculus RefresherBy A. ALBERT KLAF DOVER PUBLICATIONS, INC. NEW YORK Copyright 1944 by A. Albert Klaf.
All rights reserved This Dover edition, first published in 1956, is an unabridged and unaltered republication of the work originally published in 1944 by Whittlesey House, a division of the McGraw-Hill Book Company, under the titleCalculus Refresher for Technical Men.Library of Congress Catalog Card Number: 57-13502International Standard Book Number eISBN 13: 9780486138602 Manufactured in the United States by Courier Corporation 20370028 www.doverpublications.com PREFACE Today the watchword is speedfor the student, the engineer, the technician, the designer, the statistician- in short, for all who desire rapid integration into a mechanized world. The primary purpose of this book, therefore, is to make available, for ready and rapid use, a refresher on the fundamental concepts, methods, and practical applications of simple calculus. It is designed, chiefly, for those who have once studied the subject in the usual lengthy volumes and have found themselves swamped by details, not easily understood and, hence, more readily forgotten.
The subject matter is divided into the two customary general sections, one on differential calculus and one on integral calculus. These are followed by a third section on applications of calculus to various fields of technology. The book omits as many nonessentials as possible and, at the same time, retains enough details to clarify fundamental concepts. For ease of comprehension, the entire subject is offered in the modern question and answer forma unique presentation of calculus. Typical examples and problems are worked out in detail to illustrate the laws and principles involved in their solution. This gives the student a sense of quick mastery of the usable fundamentals of the subject.
It is hoped that this refresher will prove adaptable as a ready reference book, especially where rapidity of attainment is essential. A. A LBERT K LAF . SECION I SIMPLE DIFFERENTIAL CALCULUS C HAPTER I CONSTANTSVARIABLESFUNCTIONS-INCREMENTS1. What is a constant? A quantity whose value is fixed. 2.
What is a numerical or absolute constant? A constant that always has the same value, as 1, 2, 7, 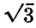 , , , etc. 3. What is an arbitrary constant? A constant that continues to have the same value throughout one problem but may have another value in a different problem. It may be represented by a letter from the beginning of the alphabet, as a, b, c, d, etc. 4. What is a variable? A quantity that may assume an indefinite number of values in the same problem and which may be represented usually by a letter from the end of the alphabet, as s,t, u, v, w, x, y, or z.5.
, , , etc. 3. What is an arbitrary constant? A constant that continues to have the same value throughout one problem but may have another value in a different problem. It may be represented by a letter from the beginning of the alphabet, as a, b, c, d, etc. 4. What is a variable? A quantity that may assume an indefinite number of values in the same problem and which may be represented usually by a letter from the end of the alphabet, as s,t, u, v, w, x, y, or z.5.
What is meant by an interval of a variable? The variable is considered confined to take on all values lying only between two numbers, as [a, b], a being less than b.6. When is a variable said to vary continuously throughan interval [a, b]? When the variable assumes in succession all possible intermediate values from a to b.7. What is a function? A function is a relationship between variables. 
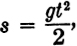 where s is the distance a body will fall in t sec. and g is the constant acceleration due to gravity, s is said to be a function of t.8. What is a dependent variable? A variable whose value depends upon the value of another variable.
where s is the distance a body will fall in t sec. and g is the constant acceleration due to gravity, s is said to be a function of t.8. What is a dependent variable? A variable whose value depends upon the value of another variable.
If y = x2 tan 30, then y is the dependent variable. It depends on the value of the variable x. If 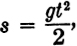 then s is the dependent variable. It depends on the value of the variable t9. What is an independent variable? A variable whose value determines the value of the related dependent variable. If y= x2 tan 30, then x is the independent variable. It determines the value of y. If
then s is the dependent variable. It depends on the value of the variable t9. What is an independent variable? A variable whose value determines the value of the related dependent variable. If y= x2 tan 30, then x is the independent variable. It determines the value of y. If 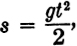 then t is the independent variable.
then t is the independent variable.
It determines the value of s. 10. What is the general relationship of the dependent and independent variables? The dependent variable is a function of the independent variable. In the above, y is a function of x; s is a function t. 11. Example In a circle whose radius is r and whose area is A, r may be assumed as depending upon A or A as depending upon r. Example In a circle whose radius is r and whose area is A, r may be assumed as depending upon A or A as depending upon r.
A change in either variable will cause a corresponding change in the other. 12. What is an implicit function? It is a function expressing an unsolved relationship between the variables.  13. What is an explicit function? A function expressing a solved relationship between the variables. y = x tan 60; y is an explicit function of x.x =
13. What is an explicit function? A function expressing a solved relationship between the variables. y = x tan 60; y is an explicit function of x.x = 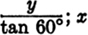 is an explicit function of y.x =
is an explicit function of y.x = 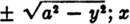 is an explicit function of y.z = a y2 tan x; z is an explicit function of y and x. The dependent variable is therefore the value of the explicit function. 14. 14.
is an explicit function of y.z = a y2 tan x; z is an explicit function of y and x. The dependent variable is therefore the value of the explicit function. 14. 14.
What are the usual symbols for expressing a function in a general way?y = f(x) is read y is a function of x and means y depends on the value of x.s = F(t) is read as is a function of t and means a depends on the value of t.u = () is read u is a, function of v and means u depends on the value of v. Other letters may also be used to express a function. Different letters are used to represent the functions when different relations exist between the variables. The same letter is used when the same relation exists though the variables are different. 15. What are the usual symbols for expressing an implicit function in a general way? F(x, y, z);f(x, y, z); (x, y, z).
Each expression indicates an implicit function in terms of x, y, z.16. What are the usual symbols for expressing an explicit function in a general way?x = F(y, z); x = f(y, z); x = (y, z). Each expression denotes x as an explicit function of y and z.17. How may the general symbol, as f(x), for a function be used to indicate substitutions for the variable in the function? If 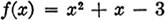 then
then 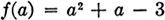 and
and 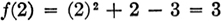 18. When is a function said to be single valued for
18. When is a function said to be single valued for
Next page













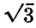 , , , etc. 3. What is an arbitrary constant? A constant that continues to have the same value throughout one problem but may have another value in a different problem. It may be represented by a letter from the beginning of the alphabet, as a, b, c, d, etc. 4. What is a variable? A quantity that may assume an indefinite number of values in the same problem and which may be represented usually by a letter from the end of the alphabet, as s,t, u, v, w, x, y, or z.5.
, , , etc. 3. What is an arbitrary constant? A constant that continues to have the same value throughout one problem but may have another value in a different problem. It may be represented by a letter from the beginning of the alphabet, as a, b, c, d, etc. 4. What is a variable? A quantity that may assume an indefinite number of values in the same problem and which may be represented usually by a letter from the end of the alphabet, as s,t, u, v, w, x, y, or z.5.
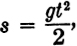 where s is the distance a body will fall in t sec. and g is the constant acceleration due to gravity, s is said to be a function of t.8. What is a dependent variable? A variable whose value depends upon the value of another variable.
where s is the distance a body will fall in t sec. and g is the constant acceleration due to gravity, s is said to be a function of t.8. What is a dependent variable? A variable whose value depends upon the value of another variable. 13. What is an explicit function? A function expressing a solved relationship between the variables. y = x tan 60; y is an explicit function of x.x =
13. What is an explicit function? A function expressing a solved relationship between the variables. y = x tan 60; y is an explicit function of x.x = 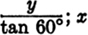 is an explicit function of y.x =
is an explicit function of y.x = 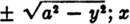 is an explicit function of y.z = a y2 tan x; z is an explicit function of y and x. The dependent variable is therefore the value of the explicit function. 14. 14.
is an explicit function of y.z = a y2 tan x; z is an explicit function of y and x. The dependent variable is therefore the value of the explicit function. 14. 14.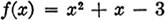 then
then 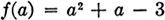 and
and 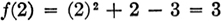 18. When is a function said to be single valued for
18. When is a function said to be single valued for