Richard A. Silverman - Introductory Complex Analysis

BIBLIOGRAPHY Ahlfors, L. V., Complex Analysis, second edition, McGraw-Hill Book Co., New York (1966). Churchill, R. V., Complex Variables and Applications, second edition, McGraw-Hill Book Co., New York (1960). Copson, E. T., An Introduction to the Theory of Functions of a Complex Variable, Oxford University Press, London (1935).

Franklin, P., Functions of a Complex Variable, Prentice-Hall, Inc., Englewood Cliffs, N.J. (1958). Hille, E., Analytic Function Theory, in two volumes, Ginn and Co., Boston (1959, 1962). Knopp, K., Theory of Functions (translated by F. Bagemihl), in two volumes, Dover Publications, Inc., New York (1945, 1947). Markushevich, A.

I., Theory of Functions of a Complex Variable (translated by R. A. Silverman), in three volumes, Prentice-Hall, Inc., Englewood Cliffs, N.J. (1965, 1967). Nehari, Z., Conformal Mapping, McGraw-Hill Book Co., New York (1952). Nehari, Z., Introduction to Complex Analysis, Allyn and Bacon, Inc., Boston (1962).

Pennisi, L. L., Elements of Complex Variables (with the collaboration of L. I. Gordon and S. Lasher), Holt, Rinehart and Winston, Inc., New York (1963). Phillips, E.

G., Functions of a Complex Variable with Applications, Oliver and Boyd, London (1961). Thron, W. J., Introduction to the Theory of Functions of a Complex Variable, John Wiley and Sons, Inc., New York (1953). Titchmarsh, E. C., The Theory of Functions, second edition, Oxford University Press, London (1939) CHAPTER COMPLEX NUMBERS, FUNCTIONS AND SEQUENCES 1. INTRODUCTORY REMARKS Since the square of a real number is nonnegative, even the simple quadratic equation has no real solutions (roots).

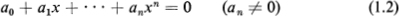However, it seems perfectly reasonable to require that any number system suitable for computational purposes allow us to solve , or, for that matter, the general algebraic equation of degree n, where a0, a1,, an are arbitrary real numbers. As already shown by () is in a certain sense the simplest algebraic equation with no real roots, an obvious first approach to our problem is to introduce an imaginary unit 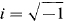, and then consider complex numbers of the form ) are treated exactly like binomials a + bx in an unknown x, except that the rule 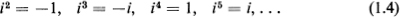is used to eliminate all powers of i higher than the first. If this is done, the roots of () include the real numbers as a special case (an essential feature). Surprisingly enough, as we shall see later ( always has a root, even if the coefficients a0, a1,, an are themselves complex numbers, a result known as the fundamental theorem of algebra. 2. COMPLEX NUMBERS AND THEIR GEOMETRIC REPRESENTATION As already noted, by a complex number we mean an expression of the form a + ib, where a and b are real numbers and i is the imaginary unit.

If c = a + ib, a is called the real part of c, written Re c, and b is called the imaginary part of c, written Im c. By the complex number zero, we mean the number 0 = 0 + i0, with zero real and imaginary parts. By definition, two complex numbers c1 and c2 are equal if and only if If Im c = 0, c = a + ib reduces to a real number, while if Im c 0, c is said to be imaginary and if Re c = 0, Im c 0, c is said to be purely imaginary. Complex numbers can be represented geometrically as points in the plane, a fact which is not only useful but virtually indispensable. Introducing a rectangular coordinate system in the plane, we can identify the complex number z = x + iy with the point P = (x, y), as shown in represent the complex numbers is called the complex plane, or the z-plane, w-plane,, depending on the letter z, w,used to denote a generic complex number. With the understanding that such a complex plane has been constructed, the terms complex number x + iy and point x + iy will be used interchangeably.

Another entirely equivalent way of representing the complex number z = x + iy is to use the vector joining the origin O of the complex plane to the point P = (x, y), instead of using the point P itself (see In other words, |z| and Arg z are the polar coordinates r and of the point with rectangular coordinates x and y, i.e., 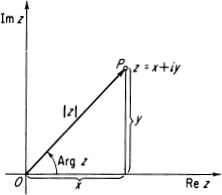FIGURE 1.1 It follows at once that 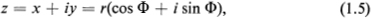where () is called the trigonometric form of the complex number z. Clearly, the quantity Arg z is defined only to within an integral multiple of 2. However, there is one and only one value of Arg z, say , which satisfies the inequality 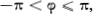and we shall call the principal value of the argument z, written arg z. The relation between Arg z and arg z is given by 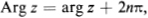where n ranges over all the integers 0, 1, 2,. It is an immediate consequence of 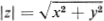and Some care is required in inverting (), since the arc tangent of a real number x, written Arc tan x, is only defined to within an integral multiple of . However, there is one and only one value of Arc tan x, say , which satisfies the inequality 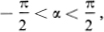and we shall call the principal value of the arc tangent of x, written arc tan x.

We can now invert the relation (), obtaining