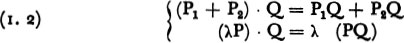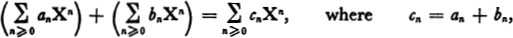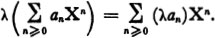Elementary Theory of Analytic Functions of One or Several Complex Variables
Henri Cartan
DOVER PUBLICATIONS, INC.
New York
Bibliographical Note
This Dover edition, first published in 1995, is an unabridged and unaltered republication of the 1973 second printing of the work first published by the Addison-Wesley Publishing Company, Reading, Massachusetts, in 1963 in the ADIWES International Series in Mathematics. It is a translation of a work originally published by Hermann, Paris, under the title Thorie lmentaire Des Fonctions Analytiques DUne Ou Plusieurs Variables Complexes.
Library of Congress Cataloging-in-Publication Data
Cartan, Henri Paul, 1904
[Thorie lmentaire des fonctions analytiques Dune ou plusieurs variables complexes. English]
Elementary theory of analytic functions of one or several complex variables / Henri Cartan.
p. cm .
An unabridged and unaltered republication of the 1973 second printing of the work first published by the Addison-Wesley Publishing Company, Reading, Massachusetts, in 1963 in the ADIWES international series in mathematicsT.p. verso.
Includes indexes.
ISBN-13: 978-0-486-68543-4 (pbk.)
ISBN-10: 0-486-68543-8 (pbk.)
1. Analytic functions.I. Title.
QA331.7.C38131995
515.9dc20
95-13507
CIP
Manufactured in the United States by Courier Corporation
68543805
www.doverpublications.com
TABLE OF CONTENTS
PREFACE
The present volume contains the substance, with some additions, of a course of lectures given at the Faculty of Science in Paris for the requirements of the licence denseignement during the academic sessions 1957-1958, 1958-1959 and 1959-1960. It is basically concerned with the theory of analytic functions of a complex variable. The case of analytic functions of several real or complex variables is, however, touched on in of the existence theorem for the solutions of differential systems in cases where the data is analytic.
The subject matter of this book covers that part of the Mathematics II certificate syllabus given to analytic functions. This same subject matter was already included in the Differential and integral calculus certificate of the old licence.
As the syllabuses of certificates for the licence are not fixed in detail, the teacher usually enjoys a considerable degree of freedom in choosing the subject matter of his course. This freedom is mainly limited by tradition and, in the case of analytic functions of a complex variable, the tradition in France is fairly well established. It will therefore perhaps be useful to indicate here to what extent I have departed from this tradition. In the first place I decided to begin by offering not Gauchys point of view (differentiable functions and Cauchys integral) but the Weiers trass point of view, i.e. the theory of convergent power series (. Here again it was thought that a few precise statements were preferable to vague intuitions and hazy ideas. On these problems of plane topology, I drew my inspiration from the excellent book by L. Ahlfors (Complex Analysis), without however conforming completely with the points of view he develops. The basic concepts of general Topology are assumed to be familiar to the reader and are employed frequently in the present work; in fact this course is addressed to students of Mathematics II who are expected to have already studied the Mathematics I syllabus.
I express my hearty thanks to Monsieur Reiji Takahashi, who are from experience gained in directing the practical work of students, has consented to supplement the various chapters of this book with exersices and problems. It is hoped that the reader will thus be in a position to make sure that he has understood and assimilated the theoretical ideas set out in the text.
HENRI CARTAN
Die (Drme), August 4th, 1960
CHAPTER I
Power Series in One Variable
1. Formal Power Series
1. ALGEBRA OF POLYNOMIALS
Let K be a commutative field. We consider the formal polynomials in one symbol (or indeterminate) X with coefficients in K (for the moment we do not give a value to X). The laws of addition of two polynomials and of multiplication of a polynomial by a scalar makes the set K[X] of polynomials into a vector space over K with the infinite base
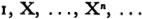
Each polynomial is a finite linear combination of the Xn with coefficients in K and we write it 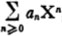 , where it is understood that only a finite number of the coefficients an are non-zero in the infinite sequence of these coefficients. The multiplication table
, where it is understood that only a finite number of the coefficients an are non-zero in the infinite sequence of these coefficients. The multiplication table
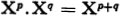
defines a multiplication in K[X]; the product
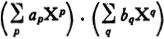
is 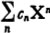 , where
, where

This multiplication is commutative and associative. It is bilinear in the sense that
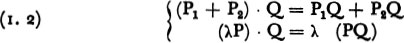
for all polynomials P, P1 P2, Q, and all scalars . It admits as unit element (denoted by 1) the polynomial 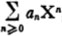 such that a0 = 1 and an = 0 for n > 0. We express all these properties by saying that K[X], provided with its vector space structure and its multiplication, is a commutative algebra with a unit element over the field K; it is, in particular, a commutative ring with a unit element.
such that a0 = 1 and an = 0 for n > 0. We express all these properties by saying that K[X], provided with its vector space structure and its multiplication, is a commutative algebra with a unit element over the field K; it is, in particular, a commutative ring with a unit element.
2. THE ALGEBRA OF FORMAL SERIES
A formal power series in X is a formal expression 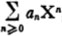 , where this time we no longer require that only a finite number of the coefficients an are non-zero. We define the sum of two formal series by
, where this time we no longer require that only a finite number of the coefficients an are non-zero. We define the sum of two formal series by
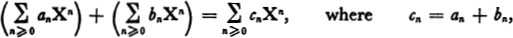
and the product of a formal series with a scalar by
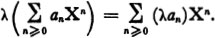
The set K[[X]] of formal series then forms a vector space over K. The neutral element of the addition is denoted by 0; it is the formal series with all its coefficients zero.
The product of two formal series is defined by the formula (), which still has a meaning because the sum on the right hand side is over a finite number of terms. The multiplication is still commutative, associative and bilinear with respect to the vector structure. Thus K[[X]] is an algebra over the field K with a unit element (denoted by 1), which is the series 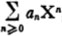
Next page













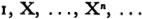
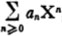 , where it is understood that only a finite number of the coefficients an are non-zero in the infinite sequence of these coefficients. The multiplication table
, where it is understood that only a finite number of the coefficients an are non-zero in the infinite sequence of these coefficients. The multiplication table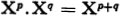
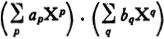
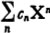 , where
, where