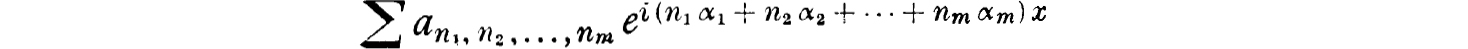Almost
PERIODIC
FUNCTIONS
HARALD BOHR
Text Translated by
Harvey Cohn
Appendixes Translated by
F. Steinhardt
DOVER PUBLICATIONS, INC.
M INEOLA , N EW Y ORK
Bibliographical Note
This Dover edition, first published in 2018, is an unabridged republication of the work originally published in 1947 by the Chelsea Publishing Company, New York.
International Standard Book Number
ISBN-13: 978-0-486-82237-2
ISBN-10: 0-486-82237-0
Manufactured in the United States by LSC Communications
82237001 2018
www.doverpublications.com
TABLE OF CONTENTS
INTRODUCTION
1. In planning the lectures which form the content of this book I had to make a choice which at first confronted me with a certain difficulty. Since the amount of time in which I had to give the lectures was rather limited, I had to decide in advance whether I wanted to give a more survey-like report on the whole theory or whether I should present only one part - but an essential one - of the theory, this, however, in fullest detail and with complete proofs. I decided for the latter alternative, holding the opinion that the lectures will be more permanently profitable for those attending if they are given the opportunity to assimilate the subject matter without haste - even if this means that the amount of material covered has to be somewhat reduced. The reduction of material was done mainly by dealing only with functions of a real variable, and besides only with continuous functions throughout.
2. In order to make up to some extent for the aforementioned reduction of material I have added two appendices to the lectures proper, as has already been said in the preface. The first of these deals with the generalization of the theory of almost periodic functions (along the lines of Lebesgues theory of the integral), while the second gives an account of the theory of almost periodic functions of a complex variable. This latter theory by the way, which has grown out of the theory of Dirichlets series, formed the authors original starting point for the entire investigation.
For the reader who wishes to go deeper into the theory there is a short bibliography at the end, listing some of the pertinent works on the subject.
3. Before starting with the presentation of the theory proper we make some preliminary remarks concerning the problems taken up in the theory of almost periodic functions. Later on, of course, there will be given a detailed and precise formulation of these problems. Generally speaking we can say that the main problem of the theory consists in finding those functions f(x) of the real variable x which are defined for < x < and which can be resolved into pure vibrations . This statement contains several words whose meanings must first of all be defined. What are pure vibrations, and what is to be understood by the word resolved? At this place I shall not go any deeper into the concept of resolution, which is most closely connected with the whole structure of the theory. However, I shall now explain precisely what is meant by a pure vibration.
4. As long as only real functions are considered, the term pure vibration applies to such functions as cosx, sin x or more generally cosx + sinx; these functions are periodic of period 2; if arbitrary periods are admitted, then pure vibration will stand for a function of the form cosx + sinx. In the following it will be more convenient for formal reasons to consider not real, but complex functions of the real variable x. By a pure vibration is then meant any function of the form aeix = a(cosx + i sinx), where a denotes an arbitrary complex number and an arbitrary real number. If a is written in the form a = |a|eiv, the function takes on the form |a|eiveix. Here |a| gives the amplitude , v the phase and the frequency of the vibration. (The period of the vibration is (for 0) 2/||). Of these numbers, |a| and are the most important; frequently |a|2 is considered instead of |a| itself.
5. The theory of almost periodic functions now deals with the following problem: Which functions f(x) can be resolved into pure vibrations on < x < i.e., are re-presentable by a trigonometric series of the form 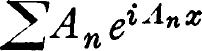 ? (We are here concerned only with series having at most denumerably many elements, or physically speaking, with functions whose spectrum is a pure line spectrum; the theory of the Fourier integral
? (We are here concerned only with series having at most denumerably many elements, or physically speaking, with functions whose spectrum is a pure line spectrum; the theory of the Fourier integral 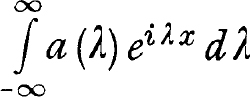 , i.e., of the continuous spectra, is, therefore not, on principle, within the scope of our problem).
, i.e., of the continuous spectra, is, therefore not, on principle, within the scope of our problem).
In the classical case where only harmonic vibrations are considered, i.e., vibrations of the form aeinx, n = 0, 1, 2, the corresponding question leads to the theory of the ordinary trigonometric series 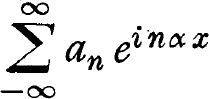 ; any periodic function of period p = 2/|| can, as is well known, be developed into such a series, the Fourier series of the function. The essentiel difference between this case and the above case where arbitrary vibrations aeix, < < were considered, lies in the fact that in the latter case the set of the frequencies which occur is non-denumerable , whereas in the first case we are from the very start dealing only with denumerably many frequencies.
; any periodic function of period p = 2/|| can, as is well known, be developed into such a series, the Fourier series of the function. The essentiel difference between this case and the above case where arbitrary vibrations aeix, < < were considered, lies in the fact that in the latter case the set of the frequencies which occur is non-denumerable , whereas in the first case we are from the very start dealing only with denumerably many frequencies.
The lectures are divided into two parts. In the first-part we take up the classical case of harmonic vibrations aeinx, choosing = 1 for simplicity, so that we are dealing with the theory of ordinary Fourier series of period 2 This part is essentially of an introductory character and is intended mainly to make for an easier and deeper understanding of the following part; because of this, the exposition differs from the usual one in some respects.
In the second part there follows a treatment of the arbitrary vibrations aeix, which leads to the general theory of almost periodic functions and of their Fourier series,
6. Bohls theory of functions periodic in the more general sense occupies an intermediate place between the theory of periodic and the theory of almost periodic functions. This theory corresponds to the case where only vibrations of the form 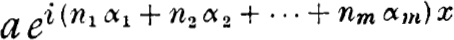 are considered, where 1, 2, . m are given linearly independent constants while n1, n2, , nm run independently through all integers 0, 1, 2, Every function periodic in the more general sense with the periods p1 = 2/|1|, p2 = 2/|2|, , pm = 2/|m| can be developed into a Fourier series of the form
are considered, where 1, 2, . m are given linearly independent constants while n1, n2, , nm run independently through all integers 0, 1, 2, Every function periodic in the more general sense with the periods p1 = 2/|1|, p2 = 2/|2|, , pm = 2/|m| can be developed into a Fourier series of the form
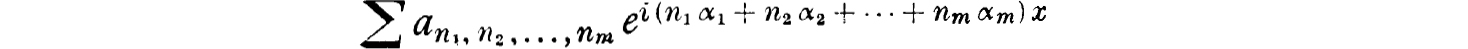
The beautiful investigations by Bohl are closely related to the theory of almost periodic functions at many points; in a certain sense, however, these Bohl functions are nearer to the pure periodic functions than to the almost periodic ones, the reason being essentially that here, again, the basic system of frequencies is denumerable.














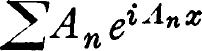 ? (We are here concerned only with series having at most denumerably many elements, or physically speaking, with functions whose spectrum is a pure line spectrum; the theory of the Fourier integral
? (We are here concerned only with series having at most denumerably many elements, or physically speaking, with functions whose spectrum is a pure line spectrum; the theory of the Fourier integral 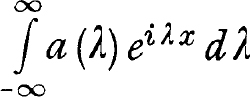 , i.e., of the continuous spectra, is, therefore not, on principle, within the scope of our problem).
, i.e., of the continuous spectra, is, therefore not, on principle, within the scope of our problem).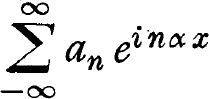 ; any periodic function of period p = 2/|| can, as is well known, be developed into such a series, the Fourier series of the function. The essentiel difference between this case and the above case where arbitrary vibrations aeix, < < were considered, lies in the fact that in the latter case the set of the frequencies which occur is non-denumerable , whereas in the first case we are from the very start dealing only with denumerably many frequencies.
; any periodic function of period p = 2/|| can, as is well known, be developed into such a series, the Fourier series of the function. The essentiel difference between this case and the above case where arbitrary vibrations aeix, < < were considered, lies in the fact that in the latter case the set of the frequencies which occur is non-denumerable , whereas in the first case we are from the very start dealing only with denumerably many frequencies.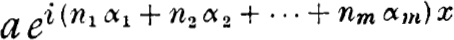 are considered, where 1, 2, . m are given linearly independent constants while n1, n2, , nm run independently through all integers 0, 1, 2, Every function periodic in the more general sense with the periods p1 = 2/|1|, p2 = 2/|2|, , pm = 2/|m| can be developed into a Fourier series of the form
are considered, where 1, 2, . m are given linearly independent constants while n1, n2, , nm run independently through all integers 0, 1, 2, Every function periodic in the more general sense with the periods p1 = 2/|1|, p2 = 2/|2|, , pm = 2/|m| can be developed into a Fourier series of the form