THEORY
OF FUNCTIONS
PARTS I AND II
KONRAD KNOPP
Translated by
FREDERICK BAGEMIHL
TWO VOLUMES BOUND AS ONE
DOVER PUBLICATIONS, INC.
MINEOLA, NEW YORK
Copyright
copyright 1945 by Dover Publications, Inc.
copyright 1947 by Dover Publications, Inc.
copyright renewed 1975 by Frederick Bagemihl. All rights reserved.
Bibliographical Note
This Dover edition, first published in 1996, is an unabridged republication in one volume of the work originally published in two volumes by Dover Publications, Inc. in 1945 ( is a new English translation of the fourth edition of Funktionentheorie, II. Teil.
Library of Congress Cataloging-in-Publication Data
Knopp, Konrad, 18821957.
[Funktionentheorie. English]
Theory of functions / Konrad Knopp; translated by Frederick Bagemihl.
p. cm.
An unabridged republication in one volume of the work originally published in two volumes by Dover Publications, Inc. in 1945 ( is a new English translation of the fourth edition of Funktionentheorie, II TeilT.p. verso.
Includes bibliographical references (p. ) and index.
Contents: pt. 1. Elements of the general theory of analytic functionspt. 2. Applications and continuation of the general theory.
ISBN 0-486-69219-1 (pbk.)
1. Functions of complex variables. I. Title.
QA331.7.K5813 1996
515.9dc20
96-12435
CIP
Manufactured in the United States by Courier Corporation
69219105
www.doverpublications.com
PART I
ELEMENTS OF THE GENERAL THEORY
OF ANALYTIC FUNCTIONS
PREFACE
This little book follows rather closely the fifth edition of Dr. Knopps Funktionentheorie. Several changes have been made in order to conform to common English terminology and notation, and to render certain passages more precise or rigorous than they are in the German volume. The proofs of in 4 were found to be incorrect, and proofs remedying this defect were substituted. Typographical errors have been corrected, the bibliography has undergone some minor changes, and a few helpful references have been added to the text.
The Translator
CONTENTS
SECTION I
FUNDAMENTAL CONCEPTS
CHAPTER 1
NUMBERS AND POINTS
1. Prerequisites
We presume that the reader is familiar with the theory of real numbers, with the foundations of real analysis (infinitesimal analysis, i.e., differential and integral calculus) which is built upon that theory, and with the elements of analytic geometry. The extent to which this is necessary in order to understand the subsequent presentation is amplified in the opening paragraphs of the Elem. and V).
Those topics of the Elem. which are most important for the present purposes will be reviewed and, in some cases, supplemented in this and the next chapter. The reader will thus be able to check for himself to what extent he possesses these prerequisites. At the same time, he will gain a firm basis for the subsequent development of the general theory of analytic functions.
2. Plane and Sphere of Complex Numbers
The set of complex numbers can be put into one-to-one correspondence with the points of a plane oriented by a rectangular coordinate system. The plane is then called the (Gaussian or complex) number plane or, more briefly, the z-plane. Every complex number z = x + iy corresponds to that point whose abscissa is the real part x = 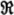 (z) and whose ordinate is the imaginary part y =
(z) and whose ordinate is the imaginary part y = 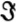 (z) =
(z) = 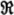 ( iz).3 As a consequence of this convention, precisely one point of the z-plane corresponds to every complex number z; and, conversely, precisely one complex number corresponds to every point of this plane. Point and number can therefore be used as equivalent expressions without fear of misinterpretations, so that we may use such expressions as the point
( iz).3 As a consequence of this convention, precisely one point of the z-plane corresponds to every complex number z; and, conversely, precisely one complex number corresponds to every point of this plane. Point and number can therefore be used as equivalent expressions without fear of misinterpretations, so that we may use such expressions as the point 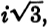 or the distance between two numbers, or the triangle with the vertices z1, z2, z3, etc.
or the distance between two numbers, or the triangle with the vertices z1, z2, z3, etc.
If r and are the polar coordinates of the point z, of z. In symbols: | z | = r, am z = .
It is useful to call special attention to the following simple facts which follow from this equivalence of point and number.
a) The distance of a point z from the origin is | z |. The distance between two points z1 and z2 is | z1z2| = | z2z1|. The number z2z1 is represented by the vector extending from the point z1 to the point z2. The relations
| zz2 | | z1 | + | z2 | and | z1z2 | 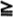
 | z1 | | z2 |
| z1 | | z2 |  hold for arbitrary z1 and z2.
hold for arbitrary z1 and z2.
b) The circumference of the circle of unit radius about the origin as center (the so-called unit circle) is characterized by | z | = 1; i.e., all numbers z for which | z | = 1 are points of this circumference, and conversely.
c) The interior of the circle of radius r about z0 as center, exclusive of its circumference (its boundary), is characterized by | zz0 | < r.
d) The interior of the circle of radius 3 about 4i as center, inclusive of its boundary, is characterized by | z + 4i | 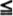 3.
3.
e) That part of the z-plane which lies outside the circle of radius R about z1 as center is given by | zz1 | > R.
f) The righthalf-plane, i.e., that part of the z-plane which lies to the right of the imaginary axis in the usual orientation of the coordinate axes, exclusive of its boundary, is characterized by 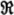 (z) > 0. Likewise, the upper half-plane, inclusive of its boundary, is given by
(z) > 0. Likewise, the upper half-plane, inclusive of its boundary, is given by 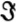 (z)
(z) 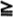 0.
0.
g) The interior of the circular ring formed by the circles of radii r and R about z0 as center, exclusive of both boundaries, is represented by 0 < r < | zz0 | < R.
h) A circle with radius about as center, briefly called a neighborhood or more precisely an -neighborhood of the point , consists of the points + z with fixed and arbitrary z subject only to the restriction | z | < (compare c)). For, setting + z = z, this means precisely that
| z | = | z | < .
The plane of complex numbers is closed by introducing an improper point, the point). Therefore the exterior of a circle (cf. e)) is also called a neighborhood of the point . For the present, however, a letter will never denote the point if the contrary is not expressly stated.















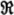 (z) and whose ordinate is the imaginary part y =
(z) and whose ordinate is the imaginary part y = 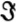 (z) =
(z) = 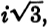 or the distance between two numbers, or the triangle with the vertices z1, z2, z3, etc.
or the distance between two numbers, or the triangle with the vertices z1, z2, z3, etc.
 | z1 | | z2 |
| z1 | | z2 |  3.
3.