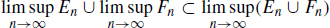Published by
Published by World Scientific Publishing Co. Pte. Ltd. 5 Toh Tuck Link, Singapore 596224
USA office: 27 Warren Street, Suite 401-402, Hackensack, NJ 07601
UK office: 51 Shelton Street, Covent Garden, London WC2H 9HE
Library of Congress Cataloging-in-Publication Data Yeh, J. Problems and proofs in real analysis : theory of measure and integration / by J. pages em Companion volume to: Real analysis: theory of measure and integration (3rd ed.). pages em Companion volume to: Real analysis: theory of measure and integration (3rd ed.).
Intended as a self-study volume. ISBN 978-981-4578-50-9 (softcover: alk. paper) 1. Mathematical analysis--Study and teaching. 2. Yeh, J. Yeh, J.
Real analysis. ll. Title. QA312.Y445 2014 515'.8--dc23 2013041974 British Library Cataloguing-in-Publication Data A catalogue record for this book is available from the British Library. Copyright 2014 by World Scientific Publishing Co. Ltd. All rights reserved. All rights reserved.
This book, or parts thereof, may not be reproduced in any form or by any means, electronic or mechanical, including photocopying, recording or any information storage and retrieval system now known or to be invented, without written permission from the publisher. For photocopying of material in this volume, please pay a copying fee through the Copyright Clearance Center, Inc., 222 Rosewood Drive, Danvers, MA 01923, USA. In this case permission to photocopy is not required from the publisher. Printed in Singapore by World Scientific Printers. To my wife
Betty ContentsPreface This volume consists of proofs of the problems in the monograph Real Analysis: Theory of Measure and Integration, 3rd Edition. Alternate proofs are included when appropriate to show different approaches to the problem or different techniques in constructing a proof. J. J.
Yeh Corona del Mar, California September, 2013 1 Measure on a -algebra of SetsProb.1.1. Given two sequences of subsets (En : n N ) and (Fn : n N ) of a set X. (a) Show that 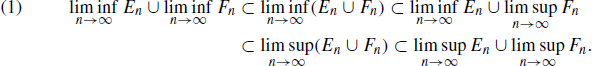 (b) Show that
(b) Show that 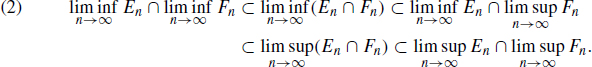 (c) Show that
(c) Show that 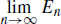 and
and 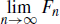 exist, then
exist, then 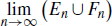 and
and 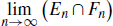 exist and moreover
exist and moreover 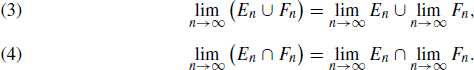 Proof. Let (An : n N ) be a sequence of subsets of X. According to Lemma 1.7,
Proof. Let (An : n N ) be a sequence of subsets of X. According to Lemma 1.7, 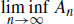 consists of every xX such that xAn for all but finitely many n N and
consists of every xX such that xAn for all but finitely many n N and 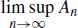 consists of every xX such that xAn for infinitely many n N . This is the basis for the proof of the chain of inclusions. 1.1. Let us prove
consists of every xX such that xAn for infinitely many n N . This is the basis for the proof of the chain of inclusions. 1.1. Let us prove 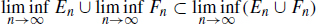 . 1.1. Let us prove
. 1.1. Let us prove 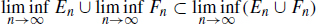 .
.
Let 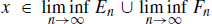 . Then we have
. Then we have 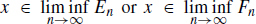 . If
. If 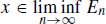 then xEn for all but finitely many n N and then xEnFn for all but finitely many n N and therefore
then xEn for all but finitely many n N and then xEnFn for all but finitely many n N and therefore 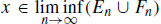 . Similarly if
. Similarly if 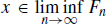 then
then 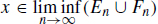 . This proves
. This proves 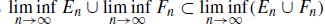 . 1.2. Let us prove
. 1.2. Let us prove 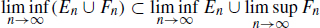 .
.
Let 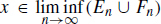 . Then xEnFn for all but finitely many n N . Suppose xFn for infinitely many n N . Then
. Then xEnFn for all but finitely many n N . Suppose xFn for infinitely many n N . Then 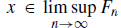 . On the other hand if xFn for only finitely many n N , then since
. On the other hand if xFn for only finitely many n N , then since 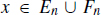 for all but finitely many n N , we must have xEn for all but finitely many n N and then
for all but finitely many n N , we must have xEn for all but finitely many n N and then 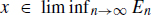 . This shows that if
. This shows that if 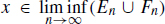 then
then 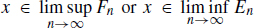 so that
so that 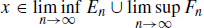 .
.
This proves 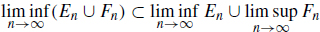 . 1.3. Let us prove
. 1.3. Let us prove 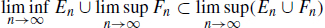 . Since
. Since 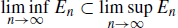 , we have
, we have 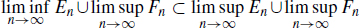 . Since EnEnFn for every n N , we have
. Since EnEnFn for every n N , we have 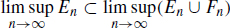 . Similarly
. Similarly 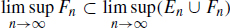 . Therefore
. Therefore 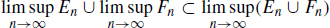














 Published by World Scientific Publishing Co. Pte. Ltd. 5 Toh Tuck Link, Singapore 596224 USA office: 27 Warren Street, Suite 401-402, Hackensack, NJ 07601 UK office: 51 Shelton Street, Covent Garden, London WC2H 9HE Library of Congress Cataloging-in-Publication Data Yeh, J. Problems and proofs in real analysis : theory of measure and integration / by J. pages em Companion volume to: Real analysis: theory of measure and integration (3rd ed.). pages em Companion volume to: Real analysis: theory of measure and integration (3rd ed.).
Published by World Scientific Publishing Co. Pte. Ltd. 5 Toh Tuck Link, Singapore 596224 USA office: 27 Warren Street, Suite 401-402, Hackensack, NJ 07601 UK office: 51 Shelton Street, Covent Garden, London WC2H 9HE Library of Congress Cataloging-in-Publication Data Yeh, J. Problems and proofs in real analysis : theory of measure and integration / by J. pages em Companion volume to: Real analysis: theory of measure and integration (3rd ed.). pages em Companion volume to: Real analysis: theory of measure and integration (3rd ed.). 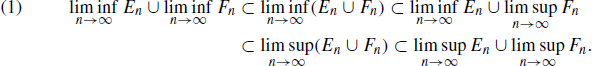 (b) Show that
(b) Show that 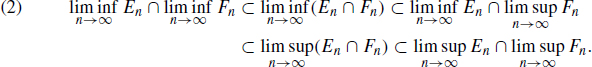 (c) Show that
(c) Show that 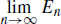 and
and 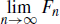 exist, then
exist, then 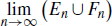 and
and 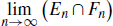 exist and moreover
exist and moreover 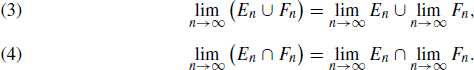 Proof. Let (An : n N ) be a sequence of subsets of X. According to Lemma 1.7,
Proof. Let (An : n N ) be a sequence of subsets of X. According to Lemma 1.7, 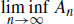 consists of every xX such that xAn for all but finitely many n N and
consists of every xX such that xAn for all but finitely many n N and 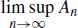 consists of every xX such that xAn for infinitely many n N . This is the basis for the proof of the chain of inclusions. 1.1. Let us prove
consists of every xX such that xAn for infinitely many n N . This is the basis for the proof of the chain of inclusions. 1.1. Let us prove 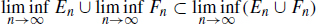 . 1.1. Let us prove
. 1.1. Let us prove 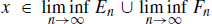 . Then we have
. Then we have 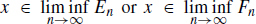 . If
. If 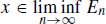 then xEn for all but finitely many n N and then xEnFn for all but finitely many n N and therefore
then xEn for all but finitely many n N and then xEnFn for all but finitely many n N and therefore 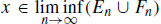 . Similarly if
. Similarly if 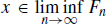 then
then 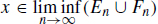 . This proves
. This proves 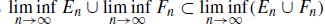 . 1.2. Let us prove
. 1.2. Let us prove 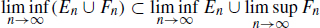 .
.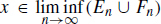 . Then xEnFn for all but finitely many n N . Suppose xFn for infinitely many n N . Then
. Then xEnFn for all but finitely many n N . Suppose xFn for infinitely many n N . Then 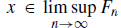 . On the other hand if xFn for only finitely many n N , then since
. On the other hand if xFn for only finitely many n N , then since 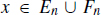 for all but finitely many n N , we must have xEn for all but finitely many n N and then
for all but finitely many n N , we must have xEn for all but finitely many n N and then 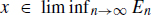 . This shows that if
. This shows that if 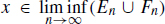 then
then 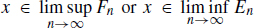 so that
so that 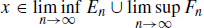 .
.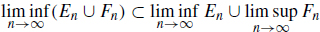 . 1.3. Let us prove
. 1.3. Let us prove 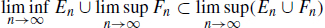 . Since
. Since 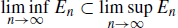 , we have
, we have 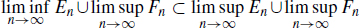 . Since EnEnFn for every n N , we have
. Since EnEnFn for every n N , we have 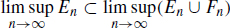 . Similarly
. Similarly 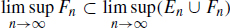 . Therefore
. Therefore