Dudziak - Vitushkins Conjecture for Removable Sets
Here you can read online Dudziak - Vitushkins Conjecture for Removable Sets full text of the book (entire story) in english for free. Download pdf and epub, get meaning, cover and reviews about this ebook. City: New York;NY, year: 2011, publisher: Springer New York : Imprint: Springer, genre: Home and family. Description of the work, (preface) as well as reviews are available. Best literature library LitArk.com created for fans of good reading and offers a wide selection of genres:
Romance novel
Science fiction
Adventure
Detective
Science
History
Home and family
Prose
Art
Politics
Computer
Non-fiction
Religion
Business
Children
Humor
Choose a favorite category and find really read worthwhile books. Enjoy immersion in the world of imagination, feel the emotions of the characters or learn something new for yourself, make an fascinating discovery.
- Book:Vitushkins Conjecture for Removable Sets
- Author:
- Publisher:Springer New York : Imprint: Springer
- Genre:
- Year:2011
- City:New York;NY
- Rating:5 / 5
- Favourites:Add to favourites
- Your mark:
Vitushkins Conjecture for Removable Sets: summary, description and annotation
We offer to read an annotation, description, summary or preface (depends on what the author of the book "Vitushkins Conjecture for Removable Sets" wrote himself). If you haven't found the necessary information about the book — write in the comments, we will try to find it.
Dudziak: author's other books
Who wrote Vitushkins Conjecture for Removable Sets? Find out the surname, the name of the author of the book and a list of all author's works by series.













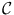 .This will be restated for emphasis many times in what follows but just as often will be tacitly assumed and not mentioned. For the sake of those readers who skip prefaces, we repeat a definition: K is removable for bounded analytic functions , or more concisely removable , if for each open superset U of K in
.This will be restated for emphasis many times in what follows but just as often will be tacitly assumed and not mentioned. For the sake of those readers who skip prefaces, we repeat a definition: K is removable for bounded analytic functions , or more concisely removable , if for each open superset U of K in 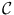 , each function that is bounded and analytic on
, each function that is bounded and analytic on 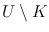 extends across K to be analytic on the whole of U . These analytic extensions must be bounded on the whole of U since they are continuous and so also bounded on K . Thus the definition may be equivalently restated as follows: K is removable if for each open superset U of K in
extends across K to be analytic on the whole of U . These analytic extensions must be bounded on the whole of U since they are continuous and so also bounded on K . Thus the definition may be equivalently restated as follows: K is removable if for each open superset U of K in 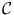 , each element of
, each element of 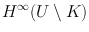 extends to an element of
extends to an element of 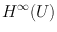 . Of course, for any open set V of
. Of course, for any open set V of 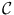 ,
, 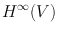 denotes the Banach algebra of all functions bounded and analytic on V . What can we say about a removable K ?
denotes the Banach algebra of all functions bounded and analytic on V . What can we say about a removable K ?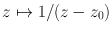 would be a function nonconstant, bounded, and analytic on
would be a function nonconstant, bounded, and analytic on 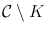 which, by Liouvilles Theorem [, 10.23], would not extend analytically to all of
which, by Liouvilles Theorem [, 10.23], would not extend analytically to all of  .
.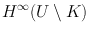 to an element of
to an element of 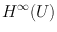 is unique and of the same supremum norm, i.e.,
is unique and of the same supremum norm, i.e., 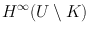 and
and 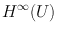 are isometrically isometric. This explains the terminology: removing K from U has made no difference to
are isometrically isometric. This explains the terminology: removing K from U has made no difference to 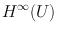 .
.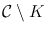 had more than one component, then the function which is one on the unbounded component and zero on all the bounded components would be a function nonconstant, bounded, and analytic on
had more than one component, then the function which is one on the unbounded component and zero on all the bounded components would be a function nonconstant, bounded, and analytic on 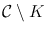 which, by Liouvilles Theorem [, 10.23], would not extend analytically to all of
which, by Liouvilles Theorem [, 10.23], would not extend analytically to all of 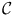 .
.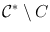 containing . Of course,
containing . Of course, 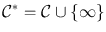 denotes the extended complex plane (also known as the Riemann sphere). By our second observation, U contains all of
denotes the extended complex plane (also known as the Riemann sphere). By our second observation, U contains all of 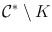 . It is an exercise in point-set topology, which we leave to the reader, to show that
. It is an exercise in point-set topology, which we leave to the reader, to show that 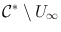 is a nontrivial connected subset of
is a nontrivial connected subset of 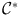 . Fix
. Fix 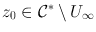 and set
and set 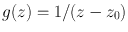 . Then
. Then 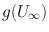 is a proper subregion of
is a proper subregion of 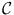 for which
for which 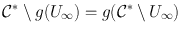 is connected. Hence, by the many equivalences to simple connectivity and the Riemann Mapping Theorem [, 10.18]. Clearly then, f does not map
is connected. Hence, by the many equivalences to simple connectivity and the Riemann Mapping Theorem [, 10.18]. Clearly then, f does not map 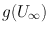 onto the open unit disc at the origin. With this contradiction we are done.
onto the open unit disc at the origin. With this contradiction we are done.