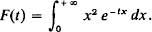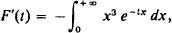Copyright 1966 by John Wiley & Sons, Inc.
Wiley Classics Library Edition Published 1995.
All rights reserved. Published simultaneously in Canada.
Reproduction or translation of any part of this work beyond that permitted by Section 107 or 108 of the 1976 United States Copyright Act without the permission of the copyright owner is unlawful. Requests for permission or further information should be addressed to the Permissions Department, John Wiley & Sons, Inc., 605 Third Avenue, New York, NY 10158-0012.
Library of Congress Cataloging in Publication Data:
Library of Congress Catalog Card Number 66-21048
ISBN 0-471-04222-6
10 9
Preface
This book consists of two separate, but closely related, parts. The first part (Chapters 1-) is subtitled The Elements of Integration; the second part (Chapters 11-17) is subtitled The Elements of Lebesgue measure. It is possible to read these two parts in either order, with only a bit of repetition.
The Elements of Integration is essentially a corrected reprint of a book with that title, originally published in 1966, designed to present the chief results of the Lebesgue theory of integration to a reader having only a modest mathematical background. This book developed from my lectures at the University of Illinois, Urbana-Champaign, and it was subsequently used there and elsewhere with considerable success. Its only prerequisites are a understanding of elementary real analysis and the ability to comprehend - arguments. We suppose that the reader has some familarity with the Riemann integral so that it is not necessary to provide motivation and detailed discussion, but we do not assume that the reader has a mastery of the subtleties of that theory. A solid course in advanced calculus, an understanding of the first third of my book The Elements of Real Analysis, or of most of my book Introduction to Real Analysis with D. R. Sherbert provides an adequate background. In preparing this new edition, I have seized the opportunity to correct certain errors, but I have resisted the temptation to insert additional material, since I believe that one of the features of this book that is most appreciated is its brevity.
The Elements of Lebesgue Measure is descended from class notes written to acquaint the reader with the theory of Lebesgue measure in the space Rp. While it is easy to find good treatments of the case p = 1, the case p > 1 is not quite as simple and is much less frequently discussed. The main ideas of Lebesgue measure are presented in detail in Chapters 10-15, although some relatively easy remarks are left to the reader as exercises. The fnal two chapters venture into the topic of nonmeasurable sets and round out the subject.
There are many expositions of the Lebesgue integral from various points of view, but I believe that the abstract measure space approach used here strikes directly towards the most important results: the convergence theorems. Further, this approach is particularly well-suited for students of probability and statistics, as well as students of analysis. Since the book is intended as an introduction, I do not follow all of the avenues that are encountered. However, I take pains not to attain brevity by leaving out important details, or assigning them to the reader.
Readers who complete this book are certainly not through, but if this book helps to speed them on their way, it has accomplished its purpose. In the References, I give some books that I believe readers can profitably explore, as well as works cited in the body of the text.
I am indebted to a number of colleagues, past and present, for their comments and suggestions; I particularly wish to mention N. T. Hamilton, G. H. Orland, C. W. Mullins, A. L. Peressini, and J. J. Uhl, Jr. I also wish to thank Professor Roy O. Davies of Leicester University for pointing out a number of errors and possible improvements.
ROBERT G. BARTLE
Ypsilanti and Urbana
November 20, 1994
Contents
The Elements of Integration
CHAPTER 1
Introduction
The theory of integration has its ancient and honorable roots in the method of exhaustion that was invented by Eudoxos and greatly developed by Archimedes for the purpose of calculating the areas and volumes of geometric figures. The later work of Newton and Leibniz enabled this method to grow into a systematic tool for such calculations.
As this theory developed, it has become less concerned with applications to geometry and elementary mechanics, for which it is entirely adequate, and more concerned with purely analytic questions, for which the classical theory of integration is not always sufficient. Thus a present-day mathematician is apt to be interested in the convergence of orthogonal expansions, or in applications to differential equations or probability. For him the classical theory of integration which culminated in the Riemann integral has been largely replaced by the theory which has grown from the pioneering work of Henri Lebesgue at the beginning of this century. The reason for this is very simple: the powerful convergence theorems associated with the Lebesgue theory of integration lead to more general, more complete, and more elegant results than the Riemann integral admits.
Lebesgues definition of the integral enlarges the collection of functions for which the integral is defined. Although this enlargement is useful in itself, its main virtue is that the theorems relating to the interchange of the limit and the integral are valid under less stringent assumptions than are required for the Riemann integral. Since one frequently needs to make such interchanges, the Lebesgue integral is more convenient to deal with than the Riemann integral. To exemplify these remarks, let the sequence (fn) of functions be defined for x > 0 by 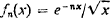 . It is readily seen that the (improper) Riemann integrals
. It is readily seen that the (improper) Riemann integrals
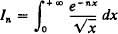
exist and that 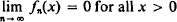 . However, since
. However, since 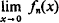 = + for each n, the convergence of the sequence is certainly not uniform for x > 0. Although it is hoped that the reader can supply the estimates required to show that lim In = 0, we prefer to obtain this conclusion as an immediate consequence of the Lebesgue Dominated Convergence Theorem which will be proved later. As anotherexample, consider the function F defined for t > 0 by the (improper) Riemann integral
= + for each n, the convergence of the sequence is certainly not uniform for x > 0. Although it is hoped that the reader can supply the estimates required to show that lim In = 0, we prefer to obtain this conclusion as an immediate consequence of the Lebesgue Dominated Convergence Theorem which will be proved later. As anotherexample, consider the function F defined for t > 0 by the (improper) Riemann integral
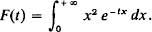
With a lntle effort one can show that F is continuous and that its derivative exists and is given by
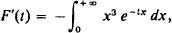
which is obtained by differentiating under the integral sign. Once again, this inference follows easily from the Lebesgue Dominated Convergence Theorem.
Next page










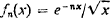 . It is readily seen that the (improper) Riemann integrals
. It is readily seen that the (improper) Riemann integrals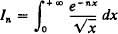
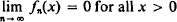 . However, since
. However, since 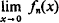 = + for each n, the convergence of the sequence is certainly not uniform for x > 0. Although it is hoped that the reader can supply the estimates required to show that lim In = 0, we prefer to obtain this conclusion as an immediate consequence of the Lebesgue Dominated Convergence Theorem which will be proved later. As anotherexample, consider the function F defined for t > 0 by the (improper) Riemann integral
= + for each n, the convergence of the sequence is certainly not uniform for x > 0. Although it is hoped that the reader can supply the estimates required to show that lim In = 0, we prefer to obtain this conclusion as an immediate consequence of the Lebesgue Dominated Convergence Theorem which will be proved later. As anotherexample, consider the function F defined for t > 0 by the (improper) Riemann integral