Toth - Measures of Symmetry for Convex Sets and Stability

Measures of Symmetry for Convex Sets and Stability — read online for free the complete book (whole text) full work

Below is the text of the book, divided by pages. System saving the place of the last page read, allows you to conveniently read the book "Measures of Symmetry for Convex Sets and Stability" online for free, without having to search again every time where you left off. Put a bookmark, and you can go to the page where you finished reading at any time.

Light

Font size:

↓

↑

Georgia Tahoma Arial Verdana

Reset

Interval:

↓

↑

Bookmark:

Make

1234567...190

Springer International Publishing Switzerland 2015

Gabor Toth Measures of Symmetry for Convex Sets and Stability Universitext 10.1007/978-3-319-23733-6_1

1. First Things First on Convex Sets

Gabor Toth 1

(1)

Department of Mathematical Sciences, Rutgers University, Camden, NJ, USA

1.1 Preliminaries

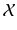A. Convex Sets. We begin here with some basic definitions and elementary facts. Throughout this book we will work in an n -dimensional real vector space . The choice of a basis in 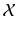amounts to a linear isomorphism 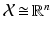, but we will make this identification only in examples and some explicit computations.

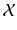We do not distinguish between the linear structure of a vector space and the underlying affine space , where the latter amounts to disregarding a distinguished point that serves as the origin.

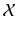Several key concepts in convexity depend on the affine structure of only. While we will occasionally indicate this by using the term affine, we will leave it to the reader to make this finer distinction to avoid a detailed and somewhat redundant introduction to affine geometry.

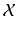Using the additive structure of , for 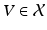, the translation 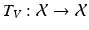with translation vector V is defined by 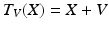, . The vector space can be naturally identified with the set 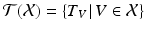of all translations of 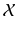(via V T V , 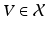), and this identification makes 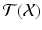a vector space (of dimension n ). We call 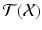the (additive) group of translations of 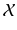. Due to their different roles, we will usually keep 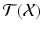and 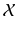separate.

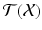Since the primary role of translations is to displace points (such as the origin in a vector space), in affine geometry is postulated to be a vector space that acts on 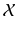(regarded only as a set) by transformations satisfying certain axioms. This defines the affine structure on .

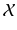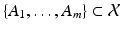An affine combination of a finite set , m 1, is a sum 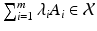with coefficients 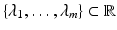satisfying .

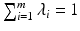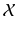As noted above, the term affine refers to the fact that affine combinations depend only on the underlying affine structure of . This means that they do not depend on the specific location of the origin, or, in other words, they are invariant under translations in the sense that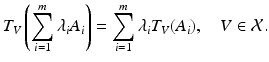

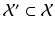A subset is an affine subspace if, along with any finite set of points 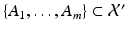, m 1, any affine combinations 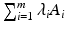, , 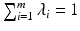, 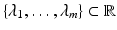also belong to .

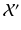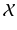An affine subspace of is a linear subspace if and only if it contains the origin. Consequently, an affine subspace in 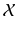is a translated copy of a linear subspace of .

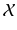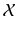The concepts of line , plane , hyperplane , etc. (corresponding to affine subspaces of dimensions 1, 2, n 1, etc.) in are readily understood.

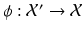An affine map between vector spaces is a map that preserves affine combinations, that is, we have

Next page

1234567...190

Light

Font size:

↓

↑

Georgia Tahoma Arial Verdana

Reset

Interval:

↓

↑

Bookmark:

Make

Similar books «Measures of Symmetry for Convex Sets and Stability»

Look at similar books to Measures of Symmetry for Convex Sets and Stability. We have selected literature similar in name and meaning in the hope of providing readers with more options to find new, interesting, not yet read works.

Jennifer Toth

The Mole People

Hans H. Jaffé

Symmetry in Chemistry

John Borawski

Avoiding War in the Nuclear Age: Confidence-Building Measures for Crisis Stability

Alejandro Garcés

Mathematical Programming for Power Systems Operation: From Theory to Applications in Python

Nisheeth K. Vishnoi

Algorithms for Convex Optimization

Rosen

Symmetry Discovered

Osborne

Locally Convex Spaces

Leonard I. E.

Solutions Manual to Accompany Geometry of Convex Sets

Çınlar Erhan

Real and Convex Analysis

Du Sautoy

Symmetry a journey into the patterns of nature

Ian Stewart

Why Beauty Is Truth: The History of Symmetry

Emily Toth

Unveiling Kate Chopin

Discussion, reviews of the book Measures of Symmetry for Convex Sets and Stability and just readers' own opinions. Leave your comments, write what you think about the work, its meaning or the main characters. Specify what exactly you liked and what you didn't like, and why you think so.