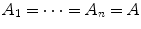This introductory chapter is devoted to general notions regarding sets, functions, sequences, and series. We aim to introduce and review the basic notation, terminology, conventions, and elementary facts.
A. Sets
A set is a collection of some objects. Given a set, the objects that form it are called its elements . Given a set A , we write x A to mean that x is an element of A . To say that x A , we also say x is in A , or x is a member of A , or x belongs to A , or A includes x .
One can specify a set by listing its elements inside curly braces, but doing so is not feasible in most cases. More often we specify a set by precisely describing its elements. For example, a,b,c } is the set whose elements are a,b , and c , and
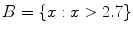
is the set of all numbers exceeding 2.7. The following are some special sets:
We assume that the reader is familiar with these sets. For example, we take it for granted that real numbers are limits of rationals.
Subsets
A set A is said to be a subset of a set B if every element of A is an element of B . We write A B or B A to indicate this and say A is contained in B , or B contains A , to the same effect. The sets A and B are the same, if and only if A B and A B , and then we write A = B . For the contrary situations, we write A B when A and B are not the same. The set A is called a proper subset of B if A is a subset of B , and A and B are not the same.
The empty set is a subset of every set. Let A be a set. The claim is that A , that is, that every element of is also an element of A , or equivalently, there is no element of that does not belong to A . But the last phrase is true simply because has no elements.
Set Operations
Let A and B be sets. Their union , denoted by A B , is the set consisting of all elements that belong to either A or B (or both). Their intersection , denoted by A B , is the set of all elements that belong to both A and B . The complement of A in B , denoted by B A , is the set of all elements of B that are not in A . Sometimes, when B is understood from context, B A is also called the complement of A and is denoted by A c . Regarding these operations, the following statements hold:
The associative laws show that A B C and A B C have unambiguous meanings.
Definitions of unions and intersections can be extended to arbitrary collections of sets. Let I be a set. For each i in I , let A i be a set. The union of the sets A i , i I , is the set A such that x A if and only if x A i for some i in I . The intersection of them is the set A such that x A if and only if x A i for every i in I . The following notations are used to denote the union and intersection respectively:
When
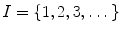
, it is customary to write
All of these notations follow the conventions for sums of numbers. For instance,
Disjoint Sets
Two sets are said to be disjoint if their intersection is empty; that is, if they have no elements in common. A collection
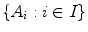
of sets is said to be disjointed if A i and A j are disjoint for every i and j in I with i j .
Products of Sets
Let A and B be sets. Their product , denoted by A B , is the set of all pairs ( x , y ) with x in A and y in B . It is also called the rectangle with sides A and B .
If
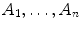
are sets, then their product

is the set of all n -tuples
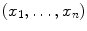
where
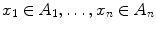
. This product is called, variously, a rectangle, or a box, or an n -dimensional box. If
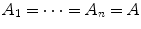













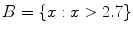 is the set of all numbers exceeding 2.7. The following are some special sets:
is the set of all numbers exceeding 2.7. The following are some special sets: 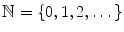 : The set of natural numbers .
: The set of natural numbers .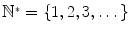 : The set of strictly positive integers .
: The set of strictly positive integers .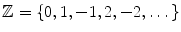 : The set of integers .
: The set of integers .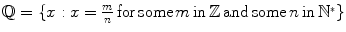 : The set of rationals .
: The set of rationals .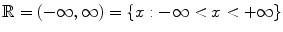 : The set of reals .
: The set of reals .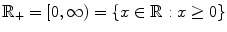 : The set of positive reals .
: The set of positive reals .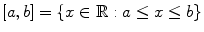 : The closed interval with endpoints a and b .
: The closed interval with endpoints a and b .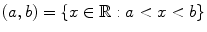 , defined for numbers a and b with a < b : The open interval with endpoints a and b .
, defined for numbers a and b with a < b : The open interval with endpoints a and b .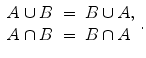
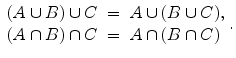
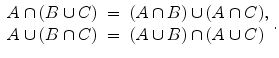
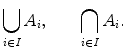
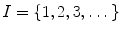 , it is customary to write
, it is customary to write 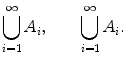
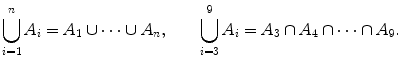
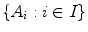 of sets is said to be disjointed if A i and A j are disjoint for every i and j in I with i j .
of sets is said to be disjointed if A i and A j are disjoint for every i and j in I with i j .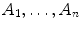 are sets, then their product
are sets, then their product  is the set of all n -tuples
is the set of all n -tuples 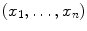 where
where 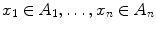 . This product is called, variously, a rectangle, or a box, or an n -dimensional box. If
. This product is called, variously, a rectangle, or a box, or an n -dimensional box. If