ADVANCED CALCULUS An Introduction to Classical Analysis ADVANCED CALCULUS An Introduction to Classical Analysis LOUIS BRAND DOVER PUBLICATIONS, INC. Mineola, New York Bibliographical Note This Dover edition, first published in 2006, is an unabridged republication of the 1967 revised printing of the work first published by John Wiley & Sons, Inc., New York, 1955. Library of Congress Cataloging-in-Publication Data Brand, Louis, 1885 Advanced calculus : an introduction to classical analysis / Louis Brand. p. cm. Originally published: New York : Wiley, 1955.
Includes index. ISBN 0-486-44548-8 (pbk.) 1. CalculusTextbooks. I. Title. 11501 Preface This book presents a course in analysis dealing essentially with functions of a real variable. 11501 Preface This book presents a course in analysis dealing essentially with functions of a real variable.
Since certain portions of real variable theory can be fully explained and comprehended only by a consideration of functions of a complex variable, one chapter has been devoted to the latter. This deals primarily with topics that are closely related to problems in the real domain, such as the removal of value barriers in real functions, disclosing relations not otherwise apparent, explaining the interval of convergence in power series, and finally the use of complex integration in computing real integrals. The opening chapter sketches the structure of the system of real and complex numbers. This may be provisionally omitted and referred to as occasion arises. The next chapter deals at length with the convergence of sequences and series. Thus some of the basic concepts of analysis are introduced in their simplest setting, through functions of an integral variable.
In the following chapters on functions of a real variable, the theory is constantly motivated and illustrated with examples. Theorems are stated in a way that is most likely to prove useful in applications, and the proofs, where lengthy, have been broken down into parts so that the logical thread is more readily followed. A course in advanced calculus should offer no hiding place for difficulties; they are frankly encountered where they arise and are dealt with as simply as possible without sacrifice of rigor. Once overcome, a difficulty often suggests a method for later use, and such parallel arguments are always carefully exploited. The fifth chapter gives a brief and self-contained introduction to vectors and the important differential invariants, gradient, divergence, and rotation. They are used in the sequel whenever the subject matter is clarified or simplified.
Since the use of vectors is now almost universal in many parts of mathematical physics, the applied mathematician should be thoroughly conversant with their properties. This applies with full force to those basic theorems that convert volume into surface integrals, surface into line integrals. These constitute a natural generalization of the fundamental theorem of the calculus, which expresses an integral over an interval in terms of function values at the end points. Since many of the subtlest and refined parts of analysis are concerned with the reversal of order in limiting processes, an entire chapter has been devoted to such considerations. This rounds out the early chapter on sequences and series and postpones many difficult parts of analysis to a point when the student has acquired some mathematical maturity. The final chapter deals with Fourier series; and this ends with Gibbs phenomenon, which affords a happy illustration of the role of precise definitions and sharp concepts in mathematics.
Because very full cross references are given in this book, an article as well as page number is given at the top of each page. Equations are numbered serially 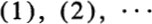 in each article. A reference to an equation in another article is made by giving article and number to the left and right of a point; thus ( is the third figure in article 160. The final article in each chapter gives a brief summary of its essential content. The student should carefully observe the distinction between necessary and sufficient conditions. If the assumption of a certain property P leads deductively to a condition C, the condition is necessary.
in each article. A reference to an equation in another article is made by giving article and number to the left and right of a point; thus ( is the third figure in article 160. The final article in each chapter gives a brief summary of its essential content. The student should carefully observe the distinction between necessary and sufficient conditions. If the assumption of a certain property P leads deductively to a condition C, the condition is necessary.
But, if the assumption of the condition C leads deductively to the property P, the condition is sufficient. Thus we have symbolically PC (necessary),C (sufficient) P. When 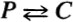 , the condition C has the admirable quality of being both necessary and sufficient. In order to hold the book to a reasonable size, some important matters were reluctantly omitted. Thus differential equations and the summability of divergent series are but casually mentioned. Moreover only Riemann integrals are considered, since the Lebesgue integral and others are now customarily introduced in the theory of functions. Finally I wish to thank my colleagues, Professors Jaeger, Jurkat, Justice, Lipsich, Lubin, and Merriman, for their suggestions in matters of exposition and for various problems.
, the condition C has the admirable quality of being both necessary and sufficient. In order to hold the book to a reasonable size, some important matters were reluctantly omitted. Thus differential equations and the summability of divergent series are but casually mentioned. Moreover only Riemann integrals are considered, since the Lebesgue integral and others are now customarily introduced in the theory of functions. Finally I wish to thank my colleagues, Professors Jaeger, Jurkat, Justice, Lipsich, Lubin, and Merriman, for their suggestions in matters of exposition and for various problems.
I am also indebted to Professor C. R. Wylie, Jr. of the University of Utah for permission to reprint his poem Paradox, which expresses so felicitously the essential nature of mathematics. L OUIS B RAND University of CincinnatiMarch 14, 1955 Contents .THE NUMBER SYSTEM .SEQUENCES AND SERIES Binomial Series .FUNCTIONS OF A REAL VARIABLE .FUNCTIONS OF SEVERAL VARIABLES Coordinate Transformations .VECTORS .THE DEFINITE INTEGRAL Repeated Integrals .IMPROPER INTEGRALS .LINE INTEGRALS .MULTIPLE INTEGRALS .UNIFORM CONVERGENCE Integrals in a Sequence .FUNCTIONS OF A COMPLEX VARIABLE .FOURIER SERIES Approximation Theorems PARADOX Not truth, nor certainty. These I foreswore In my novitiate, as young men called To holy orders must abjure the world.
If , then , this only I assert; And my successes are but pretty chains Linking twin doubts, for it is vain to ask If what I postulate be justified, Or what I prove possess the stamp of fact. Yet bridges stand, and men no longer crawl In two dimensions. And such triumphs stem In no small measure from the power this game, Played with the thrice-attenuated shades Of things, has over their originals. How frail the wand, but how profound the spell! C LARENCE R. W YLIE , J R . CHAPTER1 The Number System 1.
Groups.An equivalence relation (=) between mathematical elements 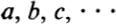 (such as numbers, matrices, permutations) must be E1 (reflexive): a = a; E2 (symmetric): a = b implies b = a; E3 (transitive): a = b, b = c imply a = c. An operation
(such as numbers, matrices, permutations) must be E1 (reflexive): a = a; E2 (symmetric): a = b implies b = a; E3 (transitive): a = b, b = c imply a = c. An operation relates every ordered pair of elements a, b to a third element
relates every ordered pair of elements a, b to a third element 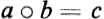 . If a = a, b = b, and
. If a = a, b = b, and 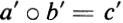 , the operation is said to be well defined if c = c. A group is composed of a finite or infinite set S of elements, an equivalence relation, and a well-defined operation (multiplication) which obeys the four postulates M1 to M4: M1 (Closure). If
, the operation is said to be well defined if c = c. A group is composed of a finite or infinite set S of elements, an equivalence relation, and a well-defined operation (multiplication) which obeys the four postulates M1 to M4: M1 (Closure). If
Next page













 in each article. A reference to an equation in another article is made by giving article and number to the left and right of a point; thus ( is the third figure in article 160. The final article in each chapter gives a brief summary of its essential content. The student should carefully observe the distinction between necessary and sufficient conditions. If the assumption of a certain property P leads deductively to a condition C, the condition is necessary.
in each article. A reference to an equation in another article is made by giving article and number to the left and right of a point; thus ( is the third figure in article 160. The final article in each chapter gives a brief summary of its essential content. The student should carefully observe the distinction between necessary and sufficient conditions. If the assumption of a certain property P leads deductively to a condition C, the condition is necessary.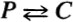 , the condition C has the admirable quality of being both necessary and sufficient. In order to hold the book to a reasonable size, some important matters were reluctantly omitted. Thus differential equations and the summability of divergent series are but casually mentioned. Moreover only Riemann integrals are considered, since the Lebesgue integral and others are now customarily introduced in the theory of functions. Finally I wish to thank my colleagues, Professors Jaeger, Jurkat, Justice, Lipsich, Lubin, and Merriman, for their suggestions in matters of exposition and for various problems.
, the condition C has the admirable quality of being both necessary and sufficient. In order to hold the book to a reasonable size, some important matters were reluctantly omitted. Thus differential equations and the summability of divergent series are but casually mentioned. Moreover only Riemann integrals are considered, since the Lebesgue integral and others are now customarily introduced in the theory of functions. Finally I wish to thank my colleagues, Professors Jaeger, Jurkat, Justice, Lipsich, Lubin, and Merriman, for their suggestions in matters of exposition and for various problems.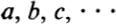 (such as numbers, matrices, permutations) must be E1 (reflexive): a = a; E2 (symmetric): a = b implies b = a; E3 (transitive): a = b, b = c imply a = c. An operation
(such as numbers, matrices, permutations) must be E1 (reflexive): a = a; E2 (symmetric): a = b implies b = a; E3 (transitive): a = b, b = c imply a = c. An operation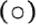 relates every ordered pair of elements a, b to a third element
relates every ordered pair of elements a, b to a third element 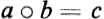 . If a = a, b = b, and
. If a = a, b = b, and 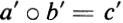 , the operation is said to be well defined if c = c. A group is composed of a finite or infinite set S of elements, an equivalence relation, and a well-defined operation (multiplication) which obeys the four postulates M1 to M4: M1 (Closure). If
, the operation is said to be well defined if c = c. A group is composed of a finite or infinite set S of elements, an equivalence relation, and a well-defined operation (multiplication) which obeys the four postulates M1 to M4: M1 (Closure). If