A.N. Kolmogorov - Foundations of the Theory of Probability

Second English Edition

A. N. Kolmogorov

Translation Edited by

Nathan Morrison

With an added Bibliography by

A. T. Bharucha-Reid

Dover Publications, Inc.

Mineola, New York

Bibliographical Note

This Dover edition, first published in 2018, is an unabridged republication of the 1956 second edition of the work originally published in 1950 by Chelsea Publishing Company, New York.

Library of Congress Cataloging-in-Publication Data

Names: Kolmogorov, A. N. (Andrei Nikolaevich), 1903-1987, author. | Bharucha-Reid, A. T. (Albert T.)

Title: Foundations of the theory of probability / A.N. Kolmogorov ; translation edited by Nathan Morrison ; with an added Bibliography by A.T. Bharucha-Reid.

Other titles: Grundbegriffe der Wahrscheinlichkeitsrechnung. English

Description: Second English edition, Dover edition. | Mineola, New York : Dover Publications, Inc., 2018. | Second English edition, originally published: New York : Chelsea Publishing Company, 1956; based on a title originally published: New York : Chelsea Publishing Company, 1950. | Includes bibliographical references.

Identifiers: LCCN 2017046438| ISBN 9780486821597 | ISBN 0486821595

Subjects: LCSH: Probabilities.

Classification: LCC QA273 .K614 2018 | DDC 519.2dc23

LC record available at https://lccn.loc.gov/2017046438

Manufactured in the United States by LSC Communications

82159501 2018

www.doverpublications.com

In the preparation of this English translation of Professor Kolmogorovs fundamental work, the original German monograph Grundbegriffe der Wahrscheinlichkeitrechnung which appeared in the Ergebnisse Der Mathematik in 1933, and also a Russian translation by G. M. Bavli published in 1936 have been used.

It is a pleasure to acknowledge the invaluable assistance of two friends and former colleagues, Mrs. Ida Rhodes and Mr. D. V. Varley, and also of my niece, Gizella Gross.

Thanks are also due to Mr. Roy Kuebler who made available for comparison purposes his independent English translation of the original German monograph.

Nathan Morrison

The purpose of this monograph is to give an axiomatic foundation for the theory of probability. The author set himself the task of putting in their natural place, among the general notions of modern mathematics, the basic concepts of probability theoryconcepts which until recently were considered to be quite peculiar.

This task would have been a rather hopeless one before the introduction of Lebesgues theories of measure and integration. However, after Lebesgues publication of his investigations, the analogies between measure of a set and probability of an event, and between integral of a function and mathematical expectation of a random variable, became apparent. These analogies allowed of further extensions; thus, for example, various properties of independent random variables were seen to be in complete analogy with the corresponding properties of orthogonal functions. But if probability theory was to be based on the above analogies, it still was necessary to make the theories of measure and integration independent of the geometric elements which were in the foreground with Lebesgue. This has been done by Frchet.

While a conception of probability theory based on the above general viewpoints has been current for some time among certain mathematicians, there was lacking a complete exposition of the whole system, free of extraneous complications. (Cf., however, the book by Frchet, [2] in the bibliography.)

I wish to call attention to those points of the present exposition which are outside the above-mentioned range of ideas familiar to the specialist. They are the following: Probability distributions in infinite-dimensional spaces (Chapter III, 4) ; differentiation and integration of mathematical expectations with respect to a parameter (Chapter IV, 5) ; and especially the theory of conditional probabilities and conditional expectations (Chapter V). It should be emphasized that these new problems arose, of necessity, from some perfectly concrete physical problems.

The sixth chapter contains a survey, without proofs, of some results of A. Khinchine and the author of the limitations on the applicability of the ordinary and of the strong law of large numbers. The bibliography contains some recent works which should be of interest from the point of view of the foundations of the subject.

I wish to express my warm thanks to Mr. Khinchine, who has read carefully the whole manuscript and proposed several improvements.

Kljasma near Moscow, Easter 1933.

A. Kolmogorov

Cf., e.g., the paper by M. Leontovich quoted in footnote 6 on p. 46; also the joint paper by the author and M. Leontovich, Zur Statistik der kontinuierlichen Systeme und des zeitlichen Verlaufes der physikalischen Vorgange. Phys. Jour, of the USSR, Vol. 3, 1933, pp. 35-63.

We define as elementary theory of probability that part of the theory in which we have to deal with probabilities of only a finite number of events. The theorems which we derive here can be applied also to the problems connected with an infinite number of random events. However, when the latter are studied, essentially new principles are used. Therefore the only axiom of the mathematical theory of probability which deals particularly with the case of an infinite number of random events is not introduced until the beginning of (Axiom VI).

The theory of probability, as a mathematical discipline, can and should be developed from axioms in exactly the same way as Geometry and Algebra. This means that after we have defined the elements to be studied and their basic relations, and have stated the axioms by which these relations are to be governed, all further exposition must be based exclusively on these axioms, independent of the usual concrete meaning of these elements and their relations.

In accordance with the above, in the concept of a field of probabilities is defined as a system of sets which satisfies certain conditions. What the elements of this set represent is of no importance in the purely mathematical development of the theory of probability (cf. the introduction of basic geometric concepts in the Foundations of Geometry by Hilbert, or the definitions of groups, rings and fields in abstract algebra).

Every axiomatic (abstract) theory admits, as is well known, of an unlimited number of concrete interpretations besides those from which it was derived. Thus we find applications in fields of science which have no relation to the concepts of random event and of probability in the precise meaning of these words.

The postulational basis of the theory of probability can be established by different methods in respect to the selection of axioms as well as in the selection of basic concepts and relations. However, if our aim is to achieve the utmost simplicity both in However, in that case, the aim is different, namely, to tie up as closely as possible the mathematical theory with the empirical development of the theory of probability.

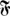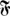
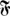Let E be a collection of elements , , ,... , which we shall call elementary events, and a set of subsets of E; the elements of the set