A Graduate Course in Probability HOWARD G. TUCKER University of California, Irvine Dover Publications, inc. Mineola, New York Copyright Copyright 1967, 1995 by Howard G. Tucker
All rights reserved. Bibliographical Note This Dover edition, first published in 2014, is an unabridged republication of the work originally published in 1967 by Academic Press, Inc., New York. Library of Congress Cataloging-in-Publication Data Tucker, Howard G., author.
A graduate course in probability / Howard G. Tucker. p. cm. Summary: Suitable for a graduate course in analytic probability, this text requires only a limited background in real analysis. Topics include probability spaces and distributions, stochastic independence, basic limiting options, strong limit theorems for independent random variables, central limit theorem, conditional expectation and Martingale theory, and an introduction to stochastic processesProvided by publisher.
Includes bibliographical references and index. eISBN-13: 978-0-486-78211-9 1. Probabilities. I. Title. QA273.T78 2014
519.2dc23 2013028059 Manufactured in the United States by Courier Corporation
49303201 2014
www.doverpublications.com To Lee Lorch Preface .
I feel that this book could serve as a text for a one-year graduate course in probability given in a mathematics program, preferably for students in their second year of graduate work. It is especially suited for a rigorous graduate course in probability needed for a mathematical statistics program. In addition, the first four chapters could be used for the first quarter of a one-year course in mathematical statistics given to mathematically mature graduate students who have never before studied probability and statistics (but who know real analysis). Last, because I have chosen to include as much explanation for the proof of each theorem as possible, and because I have resisted the urge to include anything not immediately relevant, I feel that this book could be read with profit by any mature mathematician who wishes in a reasonably short time to become acquainted with some of the basic theorems in probability. The selection of material reflects my taste for such a course. I have attempted here what I consider a proper balance between measure-theoretic aspects of probability (for example, strong limit laws, martingale theory, conditional expectation, stochastic processes) and distributional aspects (distribution functions, characteristic functions, central limit theorems).
Many important topics are omitted; for example, there is no mention of Markov chains, nor of ergodic theory, nor of Poisson processes. The material presented does not wander along any scenic byways. Rather, I was interested in traveling the shortest route to certain theorems I wished to present. These theorems are the strong limit theorems of . Material contained in all other sections and chapters of this book are results needed to provide a minimal rigorous pathway to these theorems. My primary aim in this book was to present some of the basic theorems of analytic probability theory in a cohesive manner.
I did not wish necessarily to present these in their most general and extended form. Rather, I wished to render statements of these theorems as simple as possible in order that they be easy to remember and so that the essential idea behind each proof is visible. Also I wished to put these theorems in the form most frequently referred to in research papers. Thus the presentation given here does not give the last word on any of the results. For the last word, an approach can be made through the monumental works of J. Doob, M. Doob, M.
Love, and W. Feller listed in the suggested reading section at the end of the book. I wish to call attention to the problems at the end of each section. I feel that every problem should be assigned to students taking a course in which this book is the text. The problems were designed not to increase the contents of the book but to enhance those contents already there. I feel I achieved my best success in these efforts with the problems designed for .
I wish to acknowledge my gratitude to a few of the number of people whose collective help both contributed to many smoother proofs and in several cases kept me from committing grievous errors. They are Howard H. Stratton, Jr., Lynn G. Gref, J. David Mason, William B. Koopmans. Koopmans.
The writing of this book was supported in part by the Air Force Office of Scientific Research, Grant Number AF-AFOSR 85165; this support is very much appreciated. Mrs. Jane Scully deserves my gratitude for her accurate and speedy typing of the manuscript. And, finally, I acknowledge my gratitude to Academic Press Inc. for their cooperation in this endeavor. Howard G.
Tucker Riverside, California Contents CHAPTER 1 Probability Spaces 1.1 Sigma Fields The very beginning of our considerations deals with a space or set . The set consists of elements or points, each of which is an individual outcome of a game or experiment or other random phenomenon under consideration. If the game is a toss of a die, then consists of six points. Sometimes the points of are the set of real numbers, sometimes they are a set of functions, and sometimes they are the set of all points in Euclidean n-dimensional space E(n). Each point or element in will be referred to as an elementary event, and will be called the fundamental probability set, or the sure event. In everything that follows we shall denote subsets of a fundamental probability set by upper case letters from the beginning of the English alphabet.
By 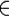 A we mean that is an elementary event in A. As usual, AB denotes the union of A and B, and AB or AB denotes the intersection of A and B. The symbol denotes the empty set. The complement of A in is denoted by Ac, and A\B denotes the set of points in A which are not in B, that is, A\B = ABc. If {Bn} is a collection of subsets, then Bn denotes their union and Bn denotes their intersection. Associated with a sure event is a nonempty set of subsets of , denoted by
A we mean that is an elementary event in A. As usual, AB denotes the union of A and B, and AB or AB denotes the intersection of A and B. The symbol denotes the empty set. The complement of A in is denoted by Ac, and A\B denotes the set of points in A which are not in B, that is, A\B = ABc. If {Bn} is a collection of subsets, then Bn denotes their union and Bn denotes their intersection. Associated with a sure event is a nonempty set of subsets of , denoted by 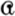 , called a sigma field (or sigma algebra) of subsets of . Definition : A set of subsets
, called a sigma field (or sigma algebra) of subsets of . Definition : A set of subsets 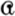 of is called a sigma field if (a) for every A
of is called a sigma field if (a) for every A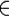
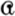 , then also Ac
, then also Ac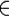
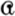 , (b) if A1, A2,..., An,... is a countable sequence of elements of
, (b) if A1, A2,..., An,... is a countable sequence of elements of 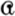 , then An
, then An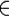
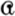 , and (c)
, and (c) 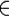
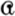 .
.
The elements or members of a sigma field 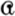 , of subsets of are called events, and much of the set-theoretic terminology is translated into the terminology of events. If the elementary event occurs and if
, of subsets of are called events, and much of the set-theoretic terminology is translated into the terminology of events. If the elementary event occurs and if 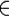 A, then we say that the event
A, then we say that the event
Next page












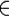 A we mean that is an elementary event in A. As usual, AB denotes the union of A and B, and AB or AB denotes the intersection of A and B. The symbol denotes the empty set. The complement of A in is denoted by Ac, and A\B denotes the set of points in A which are not in B, that is, A\B = ABc. If {Bn} is a collection of subsets, then Bn denotes their union and Bn denotes their intersection. Associated with a sure event is a nonempty set of subsets of , denoted by
A we mean that is an elementary event in A. As usual, AB denotes the union of A and B, and AB or AB denotes the intersection of A and B. The symbol denotes the empty set. The complement of A in is denoted by Ac, and A\B denotes the set of points in A which are not in B, that is, A\B = ABc. If {Bn} is a collection of subsets, then Bn denotes their union and Bn denotes their intersection. Associated with a sure event is a nonempty set of subsets of , denoted by 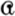 , called a sigma field (or sigma algebra) of subsets of . Definition : A set of subsets
, called a sigma field (or sigma algebra) of subsets of . Definition : A set of subsets