Shigeo Kusuoka - Stochastic Analysis

More information about this series at http://www.springer.com/series/13278 This series, consisting of research monographs and advanced textbooks for graduate students, is designed to bring together mathematicians interested in obtaining challenging new stimuli from economic theories and economists seeking effective mathematical tools for their research.

The scope of the series includes but is not limited to:

Comparable, existing monographs series are mainly organized from the viewpoint of users of mathematics, and are thus of limited interest to mathematicians. This series in contrast aims at genuine interaction between economists and mathematicians.

Most economic phenomena are described by (1) optimizing behaviors of agents (consumers, firms, governments, etc.) and (2) equilibria generated through the interactions of these agents. Consequently, the most basic mathematical subjects for economics fall into two categories:

Some fixed-point theorems and variational inequalities were created to solve the existence problem of equilibria. The stability theory and the viability theory of differential equations play important roles in the dynamic aspects of the equilibrium theory. Further, differential topology is a basic tool for the geometric analysis of equilibrium manifolds.

Economic phenomena significant in the real world often have a dynamic character. For instance, business cycles and movements of asset prices are governed by dynamic laws expressed in terms of differential or difference equations. Nonlinear analysis, harmonic analysis, and stochastic calculus play significant roles in solving dynamic economic problems. Econometric methods, including time series analysis and forecasting, also require sophisticated mathematical tools. Finally, significant developments in game theory and interaction with mathematical logic should be mentioned.

All of these topics and phenomena come within the scope of this series, aimed at cooperation between economists and mathematicians and the development of their respective disciplines.

This Springer imprint is published by the registered company Springer Nature Singapore Pte Ltd.

The registered company address is: 152 Beach Road, #21-01/04 Gateway East, Singapore 189721, Singapore

Martingale theory is now regarded as a foundation of the theory of stochastic processes. It was created essentially by Doob [2]. He refined Kolmogorovs idea on summation of independent random variables and discovered various kinds of inequalities in martingale theory. He also answered the question concerning in what case one can regard a stochastic process as a continuous process.

Martingale theory got connected with stochastic integrals and stochastic differential equations of It [5], and made great progress in the 1970s. In particular, the French school established a deep theory including discontinuous martingales. However, the theory of continuous martingales is most important for applications. The term Stochastic analysis is often used for the theory of continuous martingales, particularly in Japan.

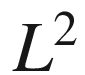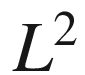There are various kinds of textbooks for stochastic analysis. However, from a viewpoint of applications (especially to finance) the content of these textbooks is either insufficient or overlong. I try to discuss stochastic analysis concisely and rigorously without reducing proofs. I try to use only elementary knowledge in functional analysis and to discuss almost all results in an framework. For example, the DoobMeyer decomposition theorem concerning submartingales is proved only in the case that submartingales are square integrable. Linear algebra and measure theory are necessary as preliminary knowledge. However, measure theory used in this book is summarized in Chap..