Pinsky - Problems from the discrete to the continuous: probability, number theory, graph theory, and combinatorics
Here you can read online Pinsky - Problems from the discrete to the continuous: probability, number theory, graph theory, and combinatorics full text of the book (entire story) in english for free. Download pdf and epub, get meaning, cover and reviews about this ebook. City: Cham, year: 2014, publisher: Springer International Publishing, genre: Children. Description of the work, (preface) as well as reviews are available. Best literature library LitArk.com created for fans of good reading and offers a wide selection of genres:
Romance novel
Science fiction
Adventure
Detective
Science
History
Home and family
Prose
Art
Politics
Computer
Non-fiction
Religion
Business
Children
Humor
Choose a favorite category and find really read worthwhile books. Enjoy immersion in the world of imagination, feel the emotions of the characters or learn something new for yourself, make an fascinating discovery.
Problems from the discrete to the continuous: probability, number theory, graph theory, and combinatorics: summary, description and annotation
We offer to read an annotation, description, summary or preface (depends on what the author of the book "Problems from the discrete to the continuous: probability, number theory, graph theory, and combinatorics" wrote himself). If you haven't found the necessary information about the book — write in the comments, we will try to find it.
Pinsky: author's other books
Who wrote Problems from the discrete to the continuous: probability, number theory, graph theory, and combinatorics? Find out the surname, the name of the author of the book and a list of all author's works by series.














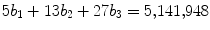 , with the restriction that b 1, b 2, b 3 be nonnegative integers? This is a specific case of the following general problem. Fix m distinct, positive integers
, with the restriction that b 1, b 2, b 3 be nonnegative integers? This is a specific case of the following general problem. Fix m distinct, positive integers 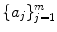 . Count the number of solutions ( b 1,, b m ) with integral entries to the equation
. Count the number of solutions ( b 1,, b m ) with integral entries to the equation 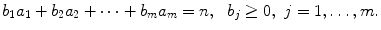
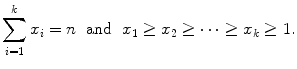
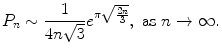
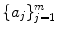 . Denote the number of such restricted partitions by
. Denote the number of such restricted partitions by 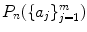 . A moments thought reveals that the number of solutions to () is
. A moments thought reveals that the number of solutions to () is 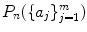 .
.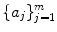 be distinct, positive integers. Assume that the greatest common divisor of
be distinct, positive integers. Assume that the greatest common divisor of 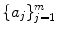 is 1: gcd(a 1 ,,a m ) = 1. Then for all sufficiently large n, there exists at least one integral solution to (). Furthermore, the number
is 1: gcd(a 1 ,,a m ) = 1. Then for all sufficiently large n, there exists at least one integral solution to (). Furthermore, the number 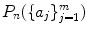 of such solutions satisfies
of such solutions satisfies 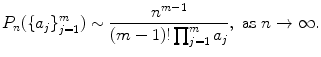
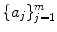 are, the more solutions there are. We also see that given m 1 and
are, the more solutions there are. We also see that given m 1 and 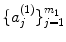 , and given m 2 and
, and given m 2 and 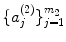 , with m 2> m 1, then for sufficiently large n there will be more solutions for the latter set of parameters.
, with m 2> m 1, then for sufficiently large n there will be more solutions for the latter set of parameters.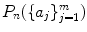 . We define the generating function of
. We define the generating function of 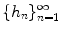 :
: 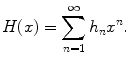
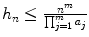 , from which it follows that the power series on the right hand side of () converges for| x |<1. See Exercise 1.1. It turns out that we can exhibit H explicitly. We demonstrate this for the case m =2, from which the general case will become clear.
, from which it follows that the power series on the right hand side of () converges for| x |<1. See Exercise 1.1. It turns out that we can exhibit H explicitly. We demonstrate this for the case m =2, from which the general case will become clear.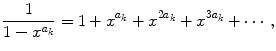
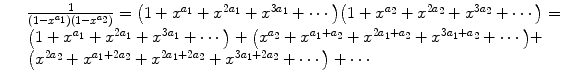
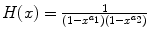 . Clearly, the same argument works for all m ; thus we conclude that
. Clearly, the same argument works for all m ; thus we conclude that 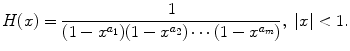
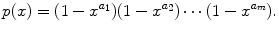
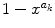 are the a k th roots of unity:
are the a k th roots of unity: