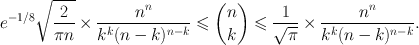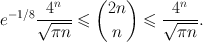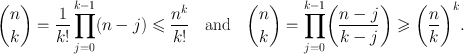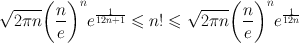Olivier Bordellès - Arithmetic Tales
Here you can read online Olivier Bordellès - Arithmetic Tales full text of the book (entire story) in english for free. Download pdf and epub, get meaning, cover and reviews about this ebook. year: 2012, publisher: Springer, genre: Children. Description of the work, (preface) as well as reviews are available. Best literature library LitArk.com created for fans of good reading and offers a wide selection of genres:
Romance novel
Science fiction
Adventure
Detective
Science
History
Home and family
Prose
Art
Politics
Computer
Non-fiction
Religion
Business
Children
Humor
Choose a favorite category and find really read worthwhile books. Enjoy immersion in the world of imagination, feel the emotions of the characters or learn something new for yourself, make an fascinating discovery.
- Book:Arithmetic Tales
- Author:
- Publisher:Springer
- Genre:
- Year:2012
- Rating:4 / 5
- Favourites:Add to favourites
- Your mark:
Arithmetic Tales: summary, description and annotation
We offer to read an annotation, description, summary or preface (depends on what the author of the book "Arithmetic Tales" wrote himself). If you haven't found the necessary information about the book — write in the comments, we will try to find it.
Number theory was once famously labeled the queen of mathematics by Gauss. The multiplicative structure of the integers in particular deals with many fascinating problems some of which are easy to understand but very difficult to solve. In the past, a variety of very different techniques has been applied to further its understanding.
Classical methods in analytic theory such as Mertens theorem and Chebyshevs inequalities and the celebrated Prime Number Theorem give estimates for the distribution of prime numbers. Later on, multiplicative structure of integers leads to multiplicative arithmetical functions for which there are many important examples in number theory. Their theory involves the Dirichlet convolution product which arises with the inclusion of several summation techniques and a survey of classical results such as Hall and Tenenbaums theorem and the Mbius Inversion Formula. Another topic is the counting integer points close to smooth curves and its relation to the distribution of squarefree numbers, which is rarely covered in existing texts. Final chapters focus on exponential sums and algebraic number fields. A number of exercises at varying levels are also included.
Topics in Multiplicative Number Theory introduces offers a comprehensive introduction into these topics with an emphasis on analytic number theory. Since it requires very little technical expertise it will appeal to a wide target group including upper level undergraduates, doctoral and masters level students.
Olivier Bordellès: author's other books
Who wrote Arithmetic Tales? Find out the surname, the name of the author of the book and a list of all author's works by series.













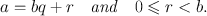

 since a S . Using Axiom 1.1 we infer that S contains a smallest element denoted by r . Thus, r is a non-negative integer and we call q the integer satisfying r = a bq .
since a S . Using Axiom 1.1 we infer that S contains a smallest element denoted by r . Thus, r is a non-negative integer and we call q the integer satisfying r = a bq .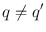 ,
,  and a = bq + r with 0 r < b . Since a = bq + r , we deduce that b ( q q )= r r , and then b | q q |=| r r |, and thus b | r r | since
and a = bq + r with 0 r < b . Since a = bq + r , we deduce that b ( q q )= r r , and then b | q q |=| r r |, and thus b | r r | since 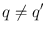 implies that | q q |1. But the inequalities 0 r < b and 0 r < b imply that | r r |< b giving a contradiction. The proof is complete.
implies that | q q |1. But the inequalities 0 r < b and 0 r < b imply that | r r |< b giving a contradiction. The proof is complete.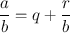
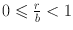 imply
imply 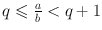 so that
so that 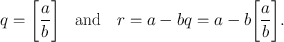
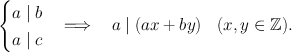
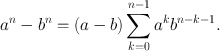
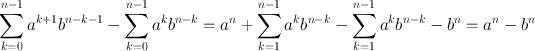
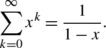
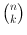 is defined by the formula
is defined by the formula 
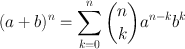
 , we have
, we have 
 , we have
, we have