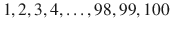Many important properties of integers were established in ancient times. In Greece, the Pythagorean school (6
century BC) studied the divisibility of numbers and considered various categories of numbers such as the primes, composite, perfect, and amicable. his Elements , Euclid (3
century BC) gives an algorithm for determining the greatest common divisor of two numbers, outlines the main properties of divisibility of integers, and proves the theorem that primes form an infinite set. Also in the 3
century BC, Eratosthenes discovered an algorithm to extract prime numbers from a series of natural numbers now called, The Sieve of Eratosthenes. There are many great names associated with the development of number theory such as Diophantus, Fermat , Descartes, Euler , Legendre, Gauss, Lagrange , to list just a few.
Over the centuries, an interest in numbers has not been entirely lost. Problems involving numbers are often included in math contests, some of which look simple but require a tremendous amounts of nonstandard thinking. Other problems look scary at first glance but allow beautiful and often short solutions.
The idea of this chapter is to develop the mathematical skills of the readers and enable them to solve unusual math problems involving integers and their properties. We will demonstrate how problems involving numbers can develop your creative thinking and how experience in solving some challenging problems will give you confidence in the subject matter.
1.1 Classification of Numbers: Even and Odd Integers
The positive whole numbers:
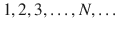
are called the natural numbers and are used for counting, e.g., there are five apples in the basket and ordering, e.g., China is the largest country in the world by population. This is the oldest defined category of numbers and the simplest in membership. In mathematical notation, we may describe the sequence of natural numbers as
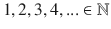
.
The second set of numbers in order of composition is the set of integers that include natural numbers and their negatives, such as
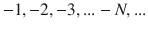
and zero 0 in order to make the operations of addition and subtraction closed on the set. The notation for this set is
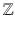
which comes from the German word, zahlen , for numbers.
The next set is the set of rational numbers ,
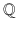
for quotient. We define a number to be rational if it can be written as a fraction
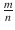
where
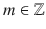
and
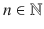
. This way we do not have to deal with divisibility by zero. Obviously, natural numbers and integers are also rational but not vice versa.
The numbers that cannot be represented by a fraction are the irrational numbers , such as
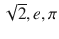
. This set does not have a special notation. Rational numbers and irrational numbers together form the set of real numbers . Descartes and Fermat (17
century) were the first to use the coordinate method to represent real numbers on the number line. Integers were discrete points on the line with whole coordinates while real numbers span a continuum, i.e., they fill out the entire number line without gaps. The introduction of real numbers allows us to perform the operations of addition, subtraction, multiplication, division (except by zero), and to raise real numbers to a power with a resultant that is also a member of the real numbers.
Finally, there is the largest set of numbers, the set of complex numbers
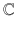
. This set contains numbers of the type
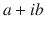
, where
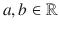
and i is an imaginary unit, such that
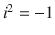
. Complex numbers geometrically are points in the plane formed by the Real and Imaginary axis. If
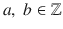
, then the complex number
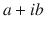
is a lattice point. We say that
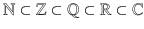
. The relationship between sets (excluding
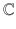
) is shown in Figure .
All natural numbers can be divided into two groups: even numbers and odd numbers . Most of us know that 3, 11, 27 are odd numbers and 20, 36, or 100 are even numbers. Let us find the general form for odd and even numbers. What is common to all even numbers such as 2, 4, 20, 2000?
Correct. They are multiples of the number 2. Therefore, we can say that every even number can be written as 2 n , where
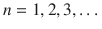
. Different values of n create different even numbers, for example,
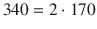
,
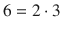
, etc.
Now let us find the general rule for an odd number. If you write all even and odd numbers together in ascending order from 1 to 100 as
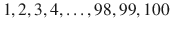












 century BC) studied the divisibility of numbers and considered various categories of numbers such as the primes, composite, perfect, and amicable. his Elements , Euclid (3
century BC) studied the divisibility of numbers and considered various categories of numbers such as the primes, composite, perfect, and amicable. his Elements , Euclid (3 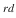 century BC) gives an algorithm for determining the greatest common divisor of two numbers, outlines the main properties of divisibility of integers, and proves the theorem that primes form an infinite set. Also in the 3
century BC) gives an algorithm for determining the greatest common divisor of two numbers, outlines the main properties of divisibility of integers, and proves the theorem that primes form an infinite set. Also in the 3 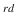 century BC, Eratosthenes discovered an algorithm to extract prime numbers from a series of natural numbers now called, The Sieve of Eratosthenes. There are many great names associated with the development of number theory such as Diophantus, Fermat , Descartes, Euler , Legendre, Gauss, Lagrange , to list just a few.
century BC, Eratosthenes discovered an algorithm to extract prime numbers from a series of natural numbers now called, The Sieve of Eratosthenes. There are many great names associated with the development of number theory such as Diophantus, Fermat , Descartes, Euler , Legendre, Gauss, Lagrange , to list just a few.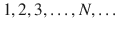 are called the natural numbers and are used for counting, e.g., there are five apples in the basket and ordering, e.g., China is the largest country in the world by population. This is the oldest defined category of numbers and the simplest in membership. In mathematical notation, we may describe the sequence of natural numbers as
are called the natural numbers and are used for counting, e.g., there are five apples in the basket and ordering, e.g., China is the largest country in the world by population. This is the oldest defined category of numbers and the simplest in membership. In mathematical notation, we may describe the sequence of natural numbers as 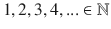 .
.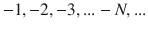 and zero 0 in order to make the operations of addition and subtraction closed on the set. The notation for this set is
and zero 0 in order to make the operations of addition and subtraction closed on the set. The notation for this set is 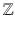 which comes from the German word, zahlen , for numbers.
which comes from the German word, zahlen , for numbers.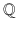 for quotient. We define a number to be rational if it can be written as a fraction
for quotient. We define a number to be rational if it can be written as a fraction 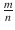 where
where 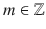 and
and 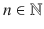 . This way we do not have to deal with divisibility by zero. Obviously, natural numbers and integers are also rational but not vice versa.
. This way we do not have to deal with divisibility by zero. Obviously, natural numbers and integers are also rational but not vice versa.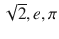 . This set does not have a special notation. Rational numbers and irrational numbers together form the set of real numbers . Descartes and Fermat (17
. This set does not have a special notation. Rational numbers and irrational numbers together form the set of real numbers . Descartes and Fermat (17 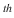 century) were the first to use the coordinate method to represent real numbers on the number line. Integers were discrete points on the line with whole coordinates while real numbers span a continuum, i.e., they fill out the entire number line without gaps. The introduction of real numbers allows us to perform the operations of addition, subtraction, multiplication, division (except by zero), and to raise real numbers to a power with a resultant that is also a member of the real numbers.
century) were the first to use the coordinate method to represent real numbers on the number line. Integers were discrete points on the line with whole coordinates while real numbers span a continuum, i.e., they fill out the entire number line without gaps. The introduction of real numbers allows us to perform the operations of addition, subtraction, multiplication, division (except by zero), and to raise real numbers to a power with a resultant that is also a member of the real numbers.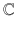 . This set contains numbers of the type
. This set contains numbers of the type 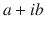 , where
, where 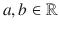 and i is an imaginary unit, such that
and i is an imaginary unit, such that 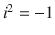 . Complex numbers geometrically are points in the plane formed by the Real and Imaginary axis. If
. Complex numbers geometrically are points in the plane formed by the Real and Imaginary axis. If 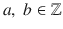 , then the complex number
, then the complex number 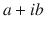 is a lattice point. We say that
is a lattice point. We say that 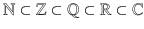 . The relationship between sets (excluding
. The relationship between sets (excluding 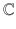 ) is shown in Figure .
) is shown in Figure . 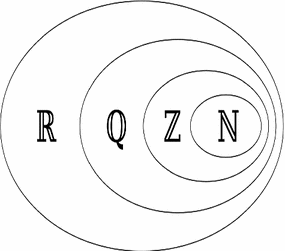
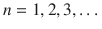 . Different values of n create different even numbers, for example,
. Different values of n create different even numbers, for example, 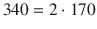 ,
, 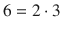 , etc.
, etc.