Chris McMullen - The Four-Color Theorem and Basic Graph Theory

The Four-Color Theorem and Basic Graph Theory — read online for free the complete book (whole text) full work

Below is the text of the book, divided by pages. System saving the place of the last page read, allows you to conveniently read the book "The Four-Color Theorem and Basic Graph Theory" online for free, without having to search again every time where you left off. Put a bookmark, and you can go to the page where you finished reading at any time.

Light

Font size:

↓

↑

Georgia Tahoma Arial Verdana

Reset

Interval:

↓

↑

Bookmark:

Make

1234567...67

The FOUR-COLOR

THEOREM

and Basic

GRAPH THEORY

Chris McMullen, Ph.D.

Copyright

The Four-Color Theorem and Basic Graph Theory

Chris McMullen, Ph.D.

Copyright 2020 Chris McMullen, Ph.D.

monkeyphysicsblog.wordpress.com

improveyourmathfluency.com

chrismcmullen.com

All rights are reserved.

Zishka Publishing

Paperback Edition ISBN: 978-1-941691-09-0

Mathematics > Four-Color Theorem

Mathematics > Graph Theory

Contents

Introduction

This book will take you on a tour of the four-color theorem and related concepts from graph theory. Numerous illustrations are provided to help you visualize important ideas. Concepts are explained in clear, simple terms. No prior knowledge of graph theory is assumed.

Following is a sample of what you will find in this book:

what the four-color theorem is

a novel explanation for why the four-color theorem holds (Chapter 27)

the reason for working with graphs instead of maps

what triangulation is and the reason behind it

visual examples of Kempe chains and Kempes attempted proof

the three-edges theorem : a simplified approach to the four-color theorem

cool concepts like quadrilateral switching and vertex splitting

the distinction between planar graphs and nonplanar graphs

how to determine if a graph is a maximal planar graph or not

Eulers formula and its relation to maximal planar graphs

explanations of Kuratowskis theorem and Wagners theorem

complete graphs and complete bipartite graphs

a survey of a few named graphs such as the Fritsch and Errera graphs

how some maximal planar graphs can be trivially colored

a simple algorithm for four-coloring a maximal planar graph (Chapters 22 and 24)

counting how many ways a graph can be colored using no more than four colors

comparing the coloring of a graph to a logic puzzle

Hamiltonian cycles and polygon forms of maximal planar graphs

what a separating triangle is and how to use it

May you enjoy this tour of the four-color theorem and basic graph theory.

1 Maps vs. Graphs

In a geography class, a map shows relationships between various regions, such as:

the border surrounding each region

the size and shape of each region

which regions share borders with one another

where one region is located relative to other regions

Notice that were using the term region . The regions could be countries on a continent, but they could be states or provinces of a nation or they could be counties that make up a state. The term region allows for generic use. Of the features mentioned above, the only one that we will be concerned with in this book is which regions share borders with one another.

In mathematics, especially as it relates to the four-color theorem (which well introduce in Chapter 2), maps and regions have slightly different meanings than they do in geography. For one, we wont allow a region to consist of two disjointed areas. For example, the United States wouldnt meet our definition of a region because Alaska and Hawaii are separated from the other 48 states. Another difference between math and geography is that we will require the regions of a map to be contiguous; there cant be gaps between the regions like lakes. A map doesnt need to show real places; we will imagine different ways maps can be drawn.

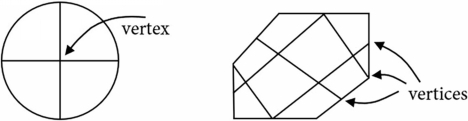
For a map, we will use the term edge to refer to any line or curve that separates one region from another region or any line or curve that separates an exterior region from the region outside of the map. Each edge begins at one vertex and ends at another vertex. Every line or curve on a map must adhere to this definition of an edge.

For a map, we will use the term vertex to refer to a point where three or more edges intersect. In plural form these points are called vertices . This definition is for a map . (When we learn about graphs, we will see that a vertex has a different definition for a graph , although it will still be a point where edges intersect.)

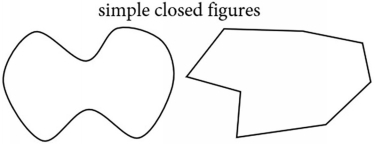
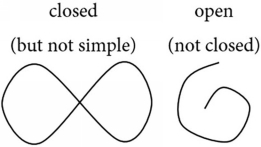
We will require each region of a map as well as the border that surrounds all of the regions to be a simple closed figure. A closed figure divides the plane into two distinct areas: the area inside the figure and the area outside the figure. In contrast, an open figure does not. By simple , we mean that the border of a single region doesnt cross itself like a figure eight; however, two different regions may join to form a figure eight. Some common examples of simple closed figures include circles, polygons, and ellipses, but the regions dont need to be common shapes; they just need to be simple closed figures.

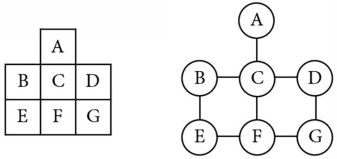
The only information that a map contains which is relevant to the four-color theorem (to be introduced in Chapter 2) is which regions share borders with which other regions. As far as this is concerned, it is simpler to redraw a map in the form of a graph . The distinction between a graph and a map is that a graph only shows which regions are neighbors; it doesnt show the size or shape of regions, relative locations, or other information that we wont need.

Any map can be represented by a graph as follows:

For each region of the map, on the graph we will draw a small circle and place the corresponding label inside of it.

For each pair of regions on the map that share an edge, on the graph we will connect these corresponding circles with a line or curve.

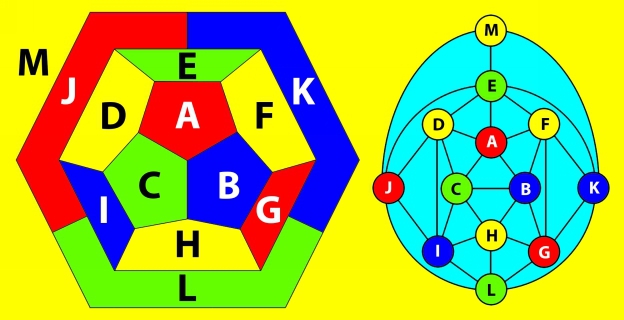
The example below shows a map on the left and its corresponding graph on the right.

Notice how a graph corresponds to a map:

On a map, each region is a face (a simple closed figure surrounded by edges). On a graph, each region is a vertex (a small circle where edges intersect).

On a map, adjacent regions share an edge. On a graph, the edges indicate which pairs of regions share edges on the map. Any line or curve that connects two vertices on a graph is considered to be an edge .

On a map, three or more edges intersect at a point called a vertex. On a graph, three or more edges surround a face .

Next page

1234567...67

Light

Font size:

↓

↑

Georgia Tahoma Arial Verdana

Reset

Interval:

↓

↑

Bookmark:

Make

Similar books «The Four-Color Theorem and Basic Graph Theory»

Look at similar books to The Four-Color Theorem and Basic Graph Theory. We have selected literature similar in name and meaning in the hope of providing readers with more options to find new, interesting, not yet read works.

A. W. Moore

Gödels Theorem

Simon Singh

Fermats Last Theorem

Chris McMullen

Geometry Proofs Essential Practice Problems Workbook with Full Solutions (Improve Your Math Fluency)

Celso Melchiades Doria

Differentiability in Banach Spaces, Differential Forms and Applications

Pinsky

Problems from the discrete to the continuous: probability, number theory, graph theory, and combinatorics

Wilson

Eulers pioneering equation: the most beautiful theorem in mathematics

Hahn

The metaphysics of the Pythagorean theorem: Thales, Pythagoras, engineering, diagrams, and the construction of the cosmos out of right triangles

Dan Morris

Bayes’ Theorem Examples : A visual introduction for beginners

R. H. Dyer

From Real to Complex Analysis

Adam Bowers

An Introductory Course in Functional Analysis

Cédric Villani

Birth of a Theorem: A Mathematical Adventure

Richard G. Heck

Freges Theorem

Discussion, reviews of the book The Four-Color Theorem and Basic Graph Theory and just readers' own opinions. Leave your comments, write what you think about the work, its meaning or the main characters. Specify what exactly you liked and what you didn't like, and why you think so.