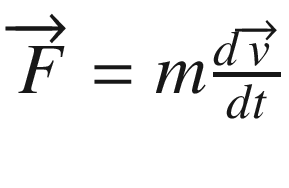Celso Melchiades Doria
Department of Mathematics, CFM, Universidade Federal de Santa Catarina, Florianpolis, Santa Catarina, Brazil
ISBN 978-3-030-77833-0 e-ISBN 978-3-030-77834-7
https://doi.org/10.1007/978-3-030-77834-7
Mathematics Subject Classication (2010): 46-01 47-01 58-01
Springer Nature Switzerland AG 2017, 2021
This work is subject to copyright. All rights are reserved by the Publisher, whether the whole or part of the material is concerned, specifically the rights of translation, reprinting, reuse of illustrations, recitation, broadcasting, reproduction on microfilms or in any other physical way, and transmission or information storage and retrieval, electronic adaptation, computer software, or by similar or dissimilar methodology now known or hereafter developed.
The use of general descriptive names, registered names, trademarks, service marks, etc. in this publication does not imply, even in the absence of a specific statement, that such names are exempt from the relevant protective laws and regulations and therefore free for general use.
The publisher, the authors and the editors are safe to assume that the advice and information in this book are believed to be true and accurate at the date of publication. Neither the publisher nor the authors or the editors give a warranty, expressed or implied, with respect to the material contained herein or for any errors or omissions that may have been made. The publisher remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
This Springer imprint is published by the registered company Springer Nature Switzerland AG
The registered company address is: Gewerbestrasse 11, 6330 Cham, Switzerland
Preface
This textbook introduces the techniques of differentiability on Banach spaces, integration of maps and some applications. In the first introduction to Calculus, the derivation and integration of the functions of one real variable are the main concern; these techniques are then extended to functions and maps of several real variables. For functions of a real variable, the main results of the theory are (a) the existence of maximum and minimum for a differentiable function defined on a compact set, and (b) the Fundamental Theorem of Calculus. When dealing with several variables, the main results are similar. Indeed, they are generalizations of cases (a) and (b), where case (b) is known as the Stokes Theorem. For functions of several variables, we should stress the importance of the Inverse Function Theorem.
The text is divided into seven chapters and three appendices. In Chap. , some applications of the Stokes Theorem and differential forms are given in the introduction to Harmonic Functions, Maxwells Equations, and Helmholtzs Theorem.
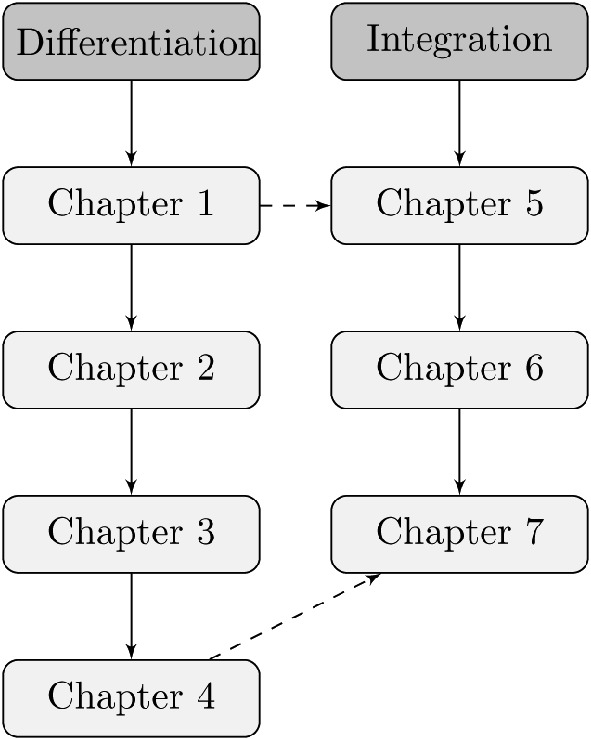
By dividing the content into two central themes (1) Differentiation and (2) Integration, we use the flowchart in Fig. to show the interdependence between chapters.
Fig.1
Chapters flowchart
There are also three appendices to make the textbook as self-contained as possible, and to support the reader in gaining an understanding of the basic terminology, the notations, the concepts and some basic theorems used in the text.
The appendices are not supposed to be read; instead they should serve as a guiding tool to recall the basics according to the needs of the readers. In Appendix A, we fix some notations, enunciate some theorems largely used throughout the other chapters, and further develop some elementary content according to our needs. In this way, Appendix A is recommended as a reference source for prerequisites and references. Appendix B introduces very basic concepts from the differentiable manifold and Lie groups. Appendix C deals with tensor algebra, which is a basic concept to have a full understanding of the content in Chap..
Celso Melchiades Doria
Florianpolis, Brazil
Introduction
At the turn of the century, at the end of 1999, there were many speculations about results of greater importance that were reached in the 1st Millenium. One day, while waiting for a medical appointment, there was a magazine listing some results that were considered to be of great significance among those obtained for the development of human knowledge. To my surprise and joy, one of the noted results was the Fundamental Theorem of Calculus. I had not thought of this possibility, but I immediately agreed to its inclusion, not only because I am a mathematician but also because it is a fact that all of Classical Mechanics, Thermodynamics and Electromagnetism were developed using calculus. Consequently, technological advancements achieved in the exact sciences and social sciences depended largely on the development of calculus.
In general, when we refer to calculus, we are discussing the techniques of differentiation and integration. In most textbooks, the study of the derivative precedes that of the integral, but not historically. The method of exhaustion developed by Archimedes was an infinite sum process, analogous to that used nowadays to define the integral of a function.
The concept of derivative of a function appeared in the sixteenth century after the emergence of analytical geometry to calculate the relative rate of change of a quantity. In the period noted, many ideas in physics were evolving rapidly due to the scientific method. In this period, the development of mechanics was latent. The Pioneers of Calculus as we know it today were Sir Isaac Newton (16421727), who developed the Method of Flows, and Gottfried Wilhelm von Leibniz (16461716) who developed Calculus, as he named it, and also gave a good part of the notation used to this day. Newton discovered the basic Laws of Classical Mechanics, then applied them together with the Method of Flows to demonstrate Keplers Laws.
Newtons 2nd Law states that a Force on a body of mass 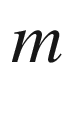 generates a relative rate of change of velocity in relation to time. More precisely, in our current mathematical language, the second Law states that the force
generates a relative rate of change of velocity in relation to time. More precisely, in our current mathematical language, the second Law states that the force 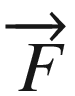 acting on a body of mass
acting on a body of mass 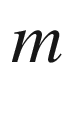 is given by
is given by 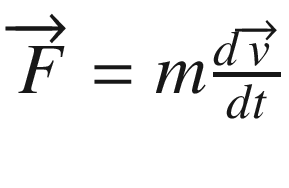




![Eisner Tanja - Operator Theoretic Aspects of Ergodic Theory [recurso electrónico] $c](/uploads/posts/book/173124/thumbs/eisner-tanja-operator-theoretic-aspects-of.jpg)








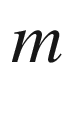 generates a relative rate of change of velocity in relation to time. More precisely, in our current mathematical language, the second Law states that the force
generates a relative rate of change of velocity in relation to time. More precisely, in our current mathematical language, the second Law states that the force 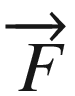 acting on a body of mass
acting on a body of mass 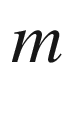 is given by
is given by