Functional Analysis by George BachmanProfessor EmeritusPolytechnic University, Brooklyn, New York and Lawrence NariciProfessorSt. Johns University, Jamaica, New York DOVER PUBLICATIONS, INC. Mineola, New York Copyright Copyright 1966, 2000 by George Bachman and Lawrence Narici All rights reserved under Pan American and International Copyright Conventions. Bibliographical Note This Dover edition, first published in 2000, is an unabridged republication of the work first published by Academic Press, New York, in 1966. A Preface to the Dover Edition and a list of errata have been added. for permission to reprint their original typography. Library of Congress Cataloging-in-Publication Data Bachman, George, 1929 Functional analysis / by George Bachman and Lawrence Narici. p. cm. cm.
This Dover edition is an unabridged republication of the work first published by Academic Press, New York, in 1966. A preface to the Dover edition and a list of errata have been addedT.p. verso. E-ISBN 0-486-40251-7 (pbk.) 1. Functional analysis. I.
Narici, Lawrence. II. Title. QA320.B24 2000 515.7dc21 00-060367 Manufactured in the United States of America Dover Publications, Inc., 31 East 2nd Street, Mineola, N.Y. 11501 Preface This book is meant to serve as an introduction to functional analysis and can be read by anyone with a background in undergraduate mathematics through the junior year. The most important courses in this undergraduate background are undoubtedly linear algebra and advanced calculus.
For the convenience of the reader, however, a brief glossary of definitions and notations relevant to linear algebra is supplied in . The only exception to these prerequisites occurs in a few examples discussed in various places throughout the text. These examples are meant for the reader with a little more mathematical maturityin particular, with some knowledge of real variables. The beginner, however, will lose nothing relevant to the main theme of development if he simply omits these examples on a first reading. We have also attempted to make the proofs of all theorems as detailed as possible and in several places have given slightly longer proofs, mainly because we felt that they were clearer and demanded less mathematical background than certain shorter versions. The exercises in most instances are meant to test the readers understanding of the text material and should be considered as an important part of the book.
In a few instances, the exercises are intended to push the readers knowledge a bit further and appropriate references are given. Thus it is hoped that the book will present a careful, detailed introductory treatment of functional analysis to the advanced undergraduate or beginning graduate mathematics major as well to those physics and engineering majors who are finding increasing applications of functional analysis in their disciplines. A second volume including such topics as topological vector spaces, Banach algebras and applications, and operator topologies is envisioned for those who might desire to pursue these matters further. Last, it is our pleasant privilege to thank some of our many friends and colleagues who encouraged us in this undertaking. In particular, our thanks go to M. Maron and H.
Allen who read the original lecture notes from which this book developed and who brought many corrections and improvements to our attention. We would also like to single out Professor George Sell who read the entire manuscript with great care and made many helpful suggestions concerning content, presentation of certain proofs, and overall clarity. His perspicacious comments were most helpful and have, we feel, enhanced the development of certain sections of the book considerably.
| Brooklyn, New York | G.B. |
| L.N. |
Preface to the Dover Edition This book is an introduction to classical functional analysis, the study of normed and inner product spaces.
To read it, you need to know linear algebra, advanced calculus and some analytic function theory for on Banach algebras. This edition is essentially the same as the 1966 Academic Press version. A list of errata appears on pages 530532. As some usage has changed, we point out that we use: 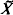 rather than X for the continuous dual of the normed space X, category I and II instead of meager and nonmeager, respectively, nowhere dense instead of rare, and generalized sequence instead of net. Having sold more than 12,000 copies (not counting the pirated editions) in English, Spanish and Korean, among others, it is almost certainly the best-selling text in the world on the subject. We want to say thank you to the many, many people who have said kind things about it.
rather than X for the continuous dual of the normed space X, category I and II instead of meager and nonmeager, respectively, nowhere dense instead of rare, and generalized sequence instead of net. Having sold more than 12,000 copies (not counting the pirated editions) in English, Spanish and Korean, among others, it is almost certainly the best-selling text in the world on the subject. We want to say thank you to the many, many people who have said kind things about it.
And thanks again for telling us about some errors and some things that could be said better. To the new reader: we wish you well. We hope you learn to love the subject the way we do. George Bachman Lawrence Narici March 2000 Contents
Functional Analysis
CHAPTER
Introduction to Inner Product Spaces
In this chapter, some of the conventions and terminology that will be adhered to throughout this book will be set down. They are listed only so that there can be no ambiguity when terms such as vector space or linear transformation are used later, and are not intended as a brief course in linear algebra. After establishing our rules, certain basic notions pertaining to inner product spaces will be touched upon.
In particular, certain inequalities and equalities will be stated. Then a rather natural extension of the notion of orthogonality of vectors from the euclidean plane is defined. Just as choosing a mutually orthogonal basis system of vectors was advantageous in two- or three-dimensional euclidean space, there are also certain advantages in dealing with orthogonal systems in higher dimensional spaces. A result proved in this chapter, known as the Gram-Schmidt process, shows that an orthogonal system of vectors can always be constructed from any denumerable set of linearly independent vectors. Focusing then more on the finite-dimensional situation, the notion of the adjoint of a linear transformation is introduced and certain of its properties are demonstrated. 1.1 Some Prerequisite Material and Conventions The most important structure in functional analysis is the vector space (linear space)a collection of objects, X, and a field F, called vectors and scalars, respectively, such that, to each pair of vectors x and y, there corresponds a third vector x + y, the sum of x and y in such a way that X constitutes an abelian group with respect to this operation.
Moreover, to each pair a and x, where a is a scalar and x is a vector, there corresponds a vector ax, called the product of and x, in such a way that 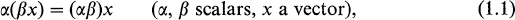
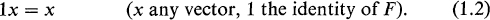 For scalars , and vectors x, y, we demand
For scalars , and vectors x, y, we demand 
 We shall often describe the above situation by saying that X is a vector space over F and shall rather strictly adhere to using lower-case italic letters (especially
We shall often describe the above situation by saying that X is a vector space over F and shall rather strictly adhere to using lower-case italic letters (especially
Next page













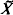 rather than X for the continuous dual of the normed space X, category I and II instead of meager and nonmeager, respectively, nowhere dense instead of rare, and generalized sequence instead of net. Having sold more than 12,000 copies (not counting the pirated editions) in English, Spanish and Korean, among others, it is almost certainly the best-selling text in the world on the subject. We want to say thank you to the many, many people who have said kind things about it.
rather than X for the continuous dual of the normed space X, category I and II instead of meager and nonmeager, respectively, nowhere dense instead of rare, and generalized sequence instead of net. Having sold more than 12,000 copies (not counting the pirated editions) in English, Spanish and Korean, among others, it is almost certainly the best-selling text in the world on the subject. We want to say thank you to the many, many people who have said kind things about it.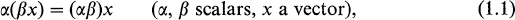
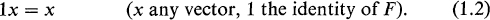 For scalars , and vectors x, y, we demand
For scalars , and vectors x, y, we demand 
 We shall often describe the above situation by saying that X is a vector space over F and shall rather strictly adhere to using lower-case italic letters (especially
We shall often describe the above situation by saying that X is a vector space over F and shall rather strictly adhere to using lower-case italic letters (especially