1. Topological Groups
Abstract
Every locally convex space is a topological group, that is, a group that is also a topological space in which the group operations (multiplication and inversion) are continuous. A large number of the most basic results about locally convex spaces are actually valid for any topological group and can be established in that context with only a little additional effort. Since topological groups are important in their own right, it seems worthwhile to establish these basic results in the context of topological groups.
1.1 Point Set Topology
Every locally convex space is a topological group, that is, a group that is also a topological space in which the group operations (multiplication and inversion) are continuous. A large number of the most basic results about locally convex spaces are actually valid for any topological group and can be established in that context with only a little additional effort. Since topological groups are important in their own right, it seems worthwhile to establish these basic results in the context of topological groups.
While the reader is assumed to be familiar with basic point set topology, there are some twists that may or may not be familiar. These are not so important for topological groups (though they are handy), but they are crucial for dealing with locally convex spaces.
A notational point should be made before proceeding. If A is a subset of a topological space, then its closure will be denoted by A . This is because we will need complex numbers, and

will denote complex conjugation. Similarly, the interior of A will be denoted by int( A ). This is because A has traditionally been assigned a special meaning in the context of locally convex spaces (it is called the polar of A ).
There are basically three subjects to be discussed. The one most likely to already be familiar is the notion of a net. While locally convex spaces can be studied without this concept, some substitute (e.g., filters) would be necessary without them.
A net is basically a generalized sequence in which the natural numbers are replaced by a directed set.
Definition 1.1.
A directed set is a pair ( D , ), where D is a nonempty set and is a binary relation on D subject to the following conditions:
(ii)
For all , , D , and implies .
(iii)
For all , D , there exists D such that and .
Note that (i) and (ii) make D look like a partially ordered set; conspicuous by its absence is the antisymmetry condition. The lack of antisymmetry is important for a number of applications (see below) and does not affect things much. The crucial addition is condition (iii), which is what the word directed usually signifies.
For some reason, it has become traditional to denote the elements of a directed set with lowercase Greek letters.
Definition 1.2.
A net in a topological space X is a function from D to X , where ( D , ) is a directed set. This function is usually denoted by x (or y , or something similar). This net x converges to x if the following happens: Whenever U is an open subset of X , with x U , then there exists D such that
Note: As usual, we sometimes refer to the directed set as D , rather than the more proper ( D , ). Similarly, means . Also, as above, the net is usually denoted by
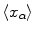
or

, and convergence to x is denoted by x x ,

, or

. Since the notion of a net is a generalization of the notion of a sequence (with
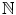
being replaced by D ), this is consistent with standard terminology for sequences.
Example 1 (cf. Bear []).
Given a bounded function
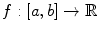
, the RiemannDarboux integral can be defined as a net limit as follows. A partition P of [ a , b ] is a finite sequence

, with

. That is, a partition is a finite set P , with
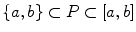
. A tagging T of the partition P above is a selection of points

for which

, and a tagged partition is an ordered pair ( P , T ) for which P is a partition and T is a tagging of P . The Riemann Sum S ( P , T , f ) for this tagged partition is the sum:
The directed set ( D , ) is the set of all tagged partitions of [ a , b ], with ( P , T ) ( P , T ) when P P . Note: The ordering ignores the tagging and so is not antisymmetric. Darbouxs version of the Riemann integral is defined as
See Bear [] for more details, including how to produce Lebesgue integrals as a net limit.
The following three facts are elementary and provide typical examples of how the flexibility in choosing D can be exploited.
Proposition 1.3.
Suppose X is a topological space. Then:
(a)
If A X, then A is the set of limits of nets from A.
(b)
X is Hausdorff if, and only if, convergent nets have unique limits.
(c)
If Y is a topological space, and f: X Y is a function, then f is continuous if, and only if, for any net

in X:

.
Proof.
(a1)
Suppose

is a net in A , and




















 will denote complex conjugation. Similarly, the interior of A will be denoted by int( A ). This is because A has traditionally been assigned a special meaning in the context of locally convex spaces (it is called the polar of A ).
will denote complex conjugation. Similarly, the interior of A will be denoted by int( A ). This is because A has traditionally been assigned a special meaning in the context of locally convex spaces (it is called the polar of A ).
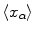 or
or  , and convergence to x is denoted by x x ,
, and convergence to x is denoted by x x ,  , or
, or  . Since the notion of a net is a generalization of the notion of a sequence (with
. Since the notion of a net is a generalization of the notion of a sequence (with 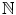 being replaced by D ), this is consistent with standard terminology for sequences.
being replaced by D ), this is consistent with standard terminology for sequences.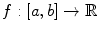 , the RiemannDarboux integral can be defined as a net limit as follows. A partition P of [ a , b ] is a finite sequence
, the RiemannDarboux integral can be defined as a net limit as follows. A partition P of [ a , b ] is a finite sequence  , with
, with  . That is, a partition is a finite set P , with
. That is, a partition is a finite set P , with 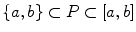 . A tagging T of the partition P above is a selection of points
. A tagging T of the partition P above is a selection of points  for which
for which  , and a tagged partition is an ordered pair ( P , T ) for which P is a partition and T is a tagging of P . The Riemann Sum S ( P , T , f ) for this tagged partition is the sum:
, and a tagged partition is an ordered pair ( P , T ) for which P is a partition and T is a tagging of P . The Riemann Sum S ( P , T , f ) for this tagged partition is the sum: 

 in X:
in X:  .
. is a net in A , and
is a net in A , and 