To my mentors, Sissa Abbati and Renzo Cirelli, who taught me the importance of rigor in mathematics, and to Brunella, Paola, Clara and Tommo, whose passion for their work has both helped and brought joy to many
From Euclidean to Hilbert Spaces
Introduction to Functional Analysis and its Applications
Edoardo Provenzi

First published 2021 in Great Britain and the United States by ISTE Ltd and John Wiley & Sons, Inc.
Apart from any fair dealing for the purposes of research or private study, or criticism or review, as permitted under the Copyright, Designs and Patents Act 1988, this publication may only be reproduced, stored or transmitted, in any form or by any means, with the prior permission in writing of the publishers, or in the case of reprographic reproduction in accordance with the terms and licenses issued by the CLA. Enquiries concerning reproduction outside these terms should be sent to the publishers at the undermentioned address:
ISTE Ltd
27-37 St Georges Road
London SW19 4EU
UK
www.iste.co.uk
John Wiley & Sons, Inc.
111 River Street
Hoboken, NJ 07030
USA
www.wiley.com
ISTE Ltd 2021
The rights of Edoardo Provenzi to be identified as the author of this work have been asserted by him in accordance with the Copyright, Designs and Patents Act 1988.
Library of Congress Control Number: 2021937006
British Library Cataloguing-in-Publication Data
A CIP record for this book is available from the British Library
ISBN 978-1-78630-682-1
Preface
This book provides an introduction to the key theoretical concepts associated with Hilbert spaces and with operators defined over these spaces.
Our decision to dedicate a whole book to the subject of Hilbert spaces stems from a simple observation: of all the infinite dimensional vector spaces, Hilbert spaces bear the closest resemblance to finite dimensional Euclidean spaces, that is, n or Cn, which provide the framework for classical analysis and linear algebra.
The topological subtleties which come into play when using infinite dimensions mean that certain conditions (which are always verified in finite dimensions) must be posed in order to maintain the validity of known results from Euclidian spaces. For Hilbert spaces, one of these topological conditions is completeness, that is, any Cauchy sequence must converge in the space in which it is defined.
From this perspective, the theory of Hilbert spaces may be seen as an elegant conjunction of algebra, analysis and topology. It draws on the work of some of the great mathematicians of the early 20th century, including Riesz, Banach and, evidently, Hilbert, who established the conditions needed to extend classical algebra and analysis into infinite dimensions.
One particularly important linear operator, the Fourier transform, appears on multiple occasions throughout this book. We start by examining the properties of this transform in finite dimensions, with the discrete Fourier transform, before extending it to infinite dimensions, considering the use of this operator in a range of different domains, including signal and image processing.
A clear understanding of the concepts introduced in this book is essential for mathematicians, physicists or engineers hoping to progress in any field, whether applied or theoretical. These concepts provide access to tools and techniques developed over a particularly rich, creative period in the history of mathematics, which remain relevant for both pure and applied forms of the subject.
The author would like to thank Olivier Husson for his assistance in producing the majority of the figures included in this book.
April 2021
Inner Product Spaces (Pre-Hilbert)
This chapter will focus on inner product spaces, that is, vector spaces with a scalar product, specifically those of finite dimension.
1.1. Real and complex inner products
In real Euclidean spaces 2 and 3, the inner product of two vectors v, w is defined as the real number:
where is the smallest angle between v and w and represents the norm (or the magnitude) of the vectors.
Using the inner product, it is possible to define the orthogonal projection of vector v in the direction defined by vector w. A distinction must be made between:
- the scalar projection of v in the direction of
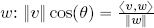 ; and
; and - the vector projection of v in the direction of
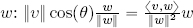 ;
;
where 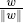 is the unit vector in the direction of w. Evidently, the roles of v and w can be reversed.
is the unit vector in the direction of w. Evidently, the roles of v and w can be reversed.
The absolute value of the scalar projection measures the similarity of the directions of two vectors. To understand this concept, consider two remarkable relative positions between v and w:
- if v and w possess the same direction, then the angle between them is either null or , hence cos() = 1, that is, the absolute value of the scalar projection of v in direction w is v;
- however, if v and w are perpendicular, then
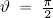 and hence cos() = 0, showing that the scalar projection of v in direction w is null.
and hence cos() = 0, showing that the scalar projection of v in direction w is null.
When the position of v relative to w falls somewhere in the interval between the two vectors described above, the absolute value of the scalar projection of v in the direction of w falls between 0 and v; this explains its use to measure the similarity of the direction of vectors.
In this book, we shall consider vector spaces which are far more complex than 2 and 3, and the measure of vector similarity obtained through projection supplies crucial information concerning the coherence of directions.
Before we can obtain this information, we must begin by moving from Euclidean spaces 2 and 3 to abstract vector spaces. The general definition of an inner product and an orthogonal projection in these spaces may be seen as an extension of the previous definitions, permitting their application to spaces in which our representation of vectors is no longer applicable.
Geometric properties, which can only be apprehended and, notably, visualized in two or three dimensions, must be replaced by a set of algebraic properties which can be used in any dimension.
Evidently, these algebraic properties must be necessary and sufficient to characterize the inner product of vectors in a plane or in real space. This approach, in which we generalize concepts which are intuitive in two or three dimensions, is a classic approach in mathematics.
In this chapter, the symbol V will be used to describe a vector space defined over the field 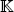
Next page














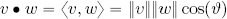
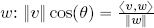 ; and
; and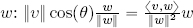 ;
;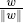 is the unit vector in the direction of w. Evidently, the roles of v and w can be reversed.
is the unit vector in the direction of w. Evidently, the roles of v and w can be reversed.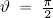 and hence cos() = 0, showing that the scalar projection of v in direction w is null.
and hence cos() = 0, showing that the scalar projection of v in direction w is null.