Table of Contents
Landmarks
Pagebreaks of the print version

 Essential Textbooks In MathematicsISSN: 2059-7657Published:
Essential Textbooks In MathematicsISSN: 2059-7657Published: A Sequential Introduction to Real Analysis
by J M Speight (University of Leeds, UK) A Friendly Approach to Functional Analysis
by Amol Sasane (London School of Economics, UK) Published by
Published by World Scientific Publishing Europe Ltd. 57 Shelton Street, Covent Garden, London WC2H 9HE
Head office: 5 Toh Tuck Link, Singapore 596224
USA office: 27 Warren Street, Suite 401-402, Hackensack, NJ 07601
Library of Congress Cataloging-in-Publication Data Names: Sasane, A. (Amol), 1976 Title: A friendly approach to functional analysis / by Amol Sasane
(London School of Economics, UK). Description: New Jersey : World Scientific, 2017. | Series: Essential textbooks in mathematics |
Includes bibliographical references and index. paper) |
ISBN 9781786343345 (softcover : alk. paper) Subjects: LCSH: Functional analysis--Textbooks. paper) Subjects: LCSH: Functional analysis--Textbooks.
Classification: LCC QA320 .S235 2017 | DDC 515/.7--dc23 LC record available at https://lccn.loc.gov/2017000443 British Library Cataloguing-in-Publication Data A catalogue record for this book is available from the British Library. Copyright 2017 by World Scientific Publishing Europe Ltd. All rights reserved. This book, or parts thereof, may not be reproduced in any form or by any means, electronic or mechanical, including photocopying, recording or any information storage and retrieval system now known or to be invented, without written permission from the Publisher. For photocopying of material in this volume, please pay a copying fee through the Copyright Clearance Center, Inc., 222 Rosewood Drive, Danvers, MA 01923, USA. In this case permission to photocopy is not required from the publisher.
What do we mean by Calculus?
It is the study of concepts involving limiting processes, such as convergence of sequences, continuity of functions, differentiation, integration, etc.
Why study Functional Analysis?
Functional analysis plays an important role in the applied sciences as well as in mathematics itself.
Why study Functional Analysis?
Functional analysis plays an important role in the applied sciences as well as in mathematics itself.
The impetus came from applications: problems related to ordinary and partial differential equations, calculus of variations, approximation theory, numerical analysis, integral equations, and so on. In ordinary calculus, one dealt with limiting processes in finite-dimensional vector spaces ( R or R d), but problems arising in the above applications required a calculus in spaces of functions (which are infinite-dimensional vector spaces). For instance, we mention the following optimisation problem as a motivating example. Example 0.1. Imagine a copper mining company which is mining in a mountain, that has an estimated amount of Q tonnes of copper, over a period of T years. Suppose that x(t) denotes the total amount of copper removed up to time t [0, T]. Since the operation is over a large time period, we may assume that this x is a function living on the continuous-time interval [0, T].
The company has the freedom to choose its mining operation: x can be any nondecreasing function on [0, T] such that x(0) = 0 (no copper removed initially) and x(T) = Q (all copper removed at the end of the mining regime). 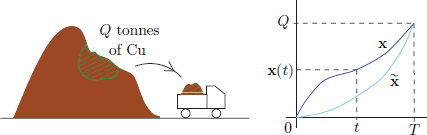 The cost of extracting copper per unit tonne at time t is
The cost of extracting copper per unit tonne at time t is 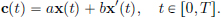 Here a, b are given positive constants. The expression is reasonable, since the term ax(t) accounts for the fact that when more and more copper is taken out, it becomes more and more difficult to find the leftover copper, while the term bx(t) accounts for the fact that if the rate of removal of copper is high, then the costs increase (for example due to machine replacement costs). We dont need to follow the exact reasoning behind this formula; this is just a model that the optimiser has been given. If the company decides on a particular mining operation x : [0, T] R , then the total cost f(x) R over the whole mining period [0, T] is given by
Here a, b are given positive constants. The expression is reasonable, since the term ax(t) accounts for the fact that when more and more copper is taken out, it becomes more and more difficult to find the leftover copper, while the term bx(t) accounts for the fact that if the rate of removal of copper is high, then the costs increase (for example due to machine replacement costs). We dont need to follow the exact reasoning behind this formula; this is just a model that the optimiser has been given. If the company decides on a particular mining operation x : [0, T] R , then the total cost f(x) R over the whole mining period [0, T] is given by 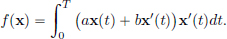 Indeed, x(t)dt is the incremental amount of copper removed at time t, and if we multiply this by c(t), we get the incremental cost at time t. The total cost should be the sum of all these incremental costs over the interval [0, T], and so we obtain the integral expression for f(x) given above.
Indeed, x(t)dt is the incremental amount of copper removed at time t, and if we multiply this by c(t), we get the incremental cost at time t. The total cost should be the sum of all these incremental costs over the interval [0, T], and so we obtain the integral expression for f(x) given above.
Hence the mining company is faced with the following natural problem: Which mining operation x incurs the least cost? In other words, minimise f : S R , where S denotes the set of all (continuously differentiable) functions x : [0, T] R such that x(0) = 0 and x(T) = Q.  Exercise 0.1. In Example 0.1, find f(x1), f(x2) where
Exercise 0.1. In Example 0.1, find f(x1), f(x2) where 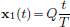 ,
, 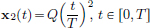 . Which is smaller among f(x1) and f(x2)? Which mining operation among x1 and x2 will be preferred?
. Which is smaller among f(x1) and f(x2)? Which mining operation among x1 and x2 will be preferred?
How do we solve optimisation problems in function spaces?
Suppose that instead of an optimisation problem in a function space, we consider a much simpler problem:
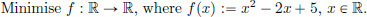
Then we know how to solve this. Indeed, from ordinary calculus, we know the following two facts.

Fact 1 allows us to narrow our choice of possible minimisers, since we can calculate
f(
x) = 2
x 2, and note that 2
x 2 = 0 if and only if
x = 1.
So if at all there is a minimiser, then it must be x = 1. On the other hand, f(x) = 2 > 0 for all x R , and so Fact 2 confirms that x = 1 is a minimiser. Thus using these two facts, we have completely solved the optimisation problem: we know that x = 1 is the only minimiser of f. 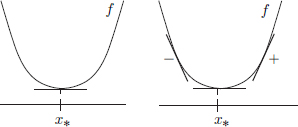














 Essential Textbooks In MathematicsISSN: 2059-7657Published: A Sequential Introduction to Real Analysis by J M Speight (University of Leeds, UK) A Friendly Approach to Functional Analysis by Amol Sasane (London School of Economics, UK)
Essential Textbooks In MathematicsISSN: 2059-7657Published: A Sequential Introduction to Real Analysis by J M Speight (University of Leeds, UK) A Friendly Approach to Functional Analysis by Amol Sasane (London School of Economics, UK) Published by World Scientific Publishing Europe Ltd. 57 Shelton Street, Covent Garden, London WC2H 9HE Head office: 5 Toh Tuck Link, Singapore 596224 USA office: 27 Warren Street, Suite 401-402, Hackensack, NJ 07601 Library of Congress Cataloging-in-Publication Data Names: Sasane, A. (Amol), 1976 Title: A friendly approach to functional analysis / by Amol Sasane
Published by World Scientific Publishing Europe Ltd. 57 Shelton Street, Covent Garden, London WC2H 9HE Head office: 5 Toh Tuck Link, Singapore 596224 USA office: 27 Warren Street, Suite 401-402, Hackensack, NJ 07601 Library of Congress Cataloging-in-Publication Data Names: Sasane, A. (Amol), 1976 Title: A friendly approach to functional analysis / by Amol Sasane The cost of extracting copper per unit tonne at time t is
The cost of extracting copper per unit tonne at time t is 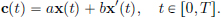 Here a, b are given positive constants. The expression is reasonable, since the term ax(t) accounts for the fact that when more and more copper is taken out, it becomes more and more difficult to find the leftover copper, while the term bx(t) accounts for the fact that if the rate of removal of copper is high, then the costs increase (for example due to machine replacement costs). We dont need to follow the exact reasoning behind this formula; this is just a model that the optimiser has been given. If the company decides on a particular mining operation x : [0, T] R , then the total cost f(x) R over the whole mining period [0, T] is given by
Here a, b are given positive constants. The expression is reasonable, since the term ax(t) accounts for the fact that when more and more copper is taken out, it becomes more and more difficult to find the leftover copper, while the term bx(t) accounts for the fact that if the rate of removal of copper is high, then the costs increase (for example due to machine replacement costs). We dont need to follow the exact reasoning behind this formula; this is just a model that the optimiser has been given. If the company decides on a particular mining operation x : [0, T] R , then the total cost f(x) R over the whole mining period [0, T] is given by 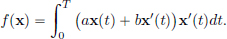 Indeed, x(t)dt is the incremental amount of copper removed at time t, and if we multiply this by c(t), we get the incremental cost at time t. The total cost should be the sum of all these incremental costs over the interval [0, T], and so we obtain the integral expression for f(x) given above.
Indeed, x(t)dt is the incremental amount of copper removed at time t, and if we multiply this by c(t), we get the incremental cost at time t. The total cost should be the sum of all these incremental costs over the interval [0, T], and so we obtain the integral expression for f(x) given above. Exercise 0.1. In Example 0.1, find f(x1), f(x2) where
Exercise 0.1. In Example 0.1, find f(x1), f(x2) where 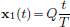 ,
, 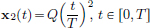 . Which is smaller among f(x1) and f(x2)? Which mining operation among x1 and x2 will be preferred?
. Which is smaller among f(x1) and f(x2)? Which mining operation among x1 and x2 will be preferred?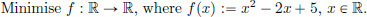 Then we know how to solve this. Indeed, from ordinary calculus, we know the following two facts.
Then we know how to solve this. Indeed, from ordinary calculus, we know the following two facts.  Fact 1 allows us to narrow our choice of possible minimisers, since we can calculate f(x) = 2x 2, and note that 2x 2 = 0 if and only if x = 1.
Fact 1 allows us to narrow our choice of possible minimisers, since we can calculate f(x) = 2x 2, and note that 2x 2 = 0 if and only if x = 1. 